Aéromodélisme RC

Techniques et conception

Détermination des ailes

avec Nurflügel

Lien vers « Sauver un animal »

Sommaire général

Auteur : Philippe Kauffmann

Version initiale : 31 décembre 2007

Dernière révision : fin février 2010

Photos : constructeur ou auteur, sauf mention contraire

N. B. : double-cliquer sur les images permet souvent d’obtenir une version agrandie.

Sommaire

Présentation de Nurflügel

Téléchargement et installation du logiciel

Principe de fonctionnement et limitations du logiciel

Le menu déroulant

Limitations

Onglet introduction des valeurs (Tragflächendefinition)

Le tableau de valeurs

Boutons radio de sélection

Onglet caractéristiques aérodynamiques (Aerodynamische Beiwerte)

Dessin des ailes

Valeurs numériques

Courbes caractéristiques

Onglet profils (Tragflächenprofile)

Choix d’un profil

Exploitation des résultats

Centrage d’un modèle

Ailes volantes

Empennage arrière

Empennage canard

Détermination d’un aéromodèle à empennage

Profil

Effilement

Flèche

Vrillage

Détermination d’une aile volante de type Fauvel

Profil

Effilement et flèche

Détermination d’une aile volante de type Horten

Profil

Effilement, flèche et vrillage

Références

Présentation de Nurflügel

            Nurflügel est un logiciel de calcul d'éléments aérodynamiques pour aéromodèles. Il est libre et gratuit, écrit et diffusé par Michael Möller (auteur du très célèbre simulateur de vol FMS). Il a été conçu au départ pour la mise au point et l'optimisation des ailes volantes, mais permet aussi le calcul de nombreux éléments utiles dans le cadre des aéromodèles classiques, à savoir :

• surface d'une aile,
• foyer géométrique d'une surface portante,
• foyer aérodynamique, c'est-à-dire le vrai foyer d'une surface portante (nécessaire pour placer correctement le centre de masse d'un modèle),
• les vitesses, incidences et coefficients aérodynamiques dans divers contextes (notamment le décrochage),
• la répartition de la portance de l’emplanture au saumon d'une aile, ce qui permet la détermination de :

· la traînée induite réelle,

· la portance réduite Ca_Max réelle d'une aile,

· la propagation du décrochage.

            Ce logiciel fonctionne uniquement sous Windows™. Il dispose d'un tutoriel de qualité sur le site d’Aerodesign [1], mais malheureusement rédigé uniquement en allemand. Aussi, ce chapitre, tutoriel simplifié, a pour but de donner aux français ignorant la langue de Goethe accès à cet excellent programme au fonctionnement au demeurant assez intuitif.

Téléchargement et installation du logiciel

La version 1.2 du logiciel peut être téléchargée à partir du site d’Aerodesign [1], à la page du tutoriel en allemand de Nurflügel. C'est une archive Winzip qui contient le programme exécutable nur.exe et quelques exemples d'ailes volantes *.fmd.

Pour utiliser le logiciel, il faut d’abord créer un répertoire au choix à l'endroit désiré. Par exemple : c:\program files\nurfluegel\. Puis il faut décompresser l'archive dans ce nouveau répertoire. Le logiciel est dès lors opérationnel. Le logiciel est toutefois plus complet si on ajoute dans son répertoire principal un sous-répertoire contenant une bibliothèque de profils comme celle de l’UIUC [2] décrite au chapitre JavaFoil.

L’outil peut être rendu plus facile d’accès si on crée un raccourci sur le bureau de Windows ou dans le menu « Démarrer » ; ce qui est surtout utile si on compte s’en servir souvent.

On pourra remarquer que la version 1.2 de Nurflügel est assez ancienne. La version actuelle 2.26 est une reprise de Franck Ranis que l’on peut trouver sur le site Zanonia [3]. Bien que les fonctionnalités restent les mêmes, l’ergonomie de cette version est très différente de celle de la version de Michael Möller car la géométrie des ailes est définie de façon différente. Certains la trouverons beaucoup plus conviviale, d’autres beaucoup moins ; question de goût. Seule la version 1.2 est décrite ici, car elle correspond plus aux goûts de l’auteur ; ce qui ne préjuge en rien des qualités de la version 2.26.

Principe de fonctionnement et limitations du logiciel

Le logiciel dispose de trois onglets. L’onglet principal (Tragflächendefinition), situé le plus à gauche permet d’entrer la définition géométrique et aérodynamique des ailes d’un modèle ; le modèle défini peut ensuite être sauvegardé dans un fichier de type *.fmd dans un répertoire au choix. On peut aussi lire un fichier de type *.fmd et le modifier pour créer un nouveau modèle.

Il faut entrer les données géométriques des ailes, mais aussi des grandeurs aérodynamiques du ou des profils utilisés, notamment ao, Cm_{0,25 ,} Ca_max et Ca_min. Une bonne estimation des deux premières grandeurs aérodynamiques peut être fournie par le troisième onglet du logiciel (Tragflächenprofile); les deux dernières devront être fournies par la fiche de chaque profil utilisé ou une soufflerie numérique comme Javafoil.

On notera à propos des diverses grandeurs que la notation des directions est fonction de la langue. Pour nous, la direction de portance est z, pour les anglais l (comme lift) et pour les allemands a (comme Auftrieb). De la même façon, la direction de trainée est notée x en français, d en anglais (comme drag) et w en allemand (comme Widerstand).

L’onglet central fournit les données calculées par Nurflügel associées aux ailes. Elles se présentent selon leur nature, soit sous forme de nombre comme la vitesse minimale de vol, soit sous forme de courbe comme la répartition de la charge alaire Ca.

Le menu déroulant

Le menu déroulant minimaliste ne comprend que trois items :

· Datei (fichier) qui contient Öffnen pour ouvrir un fichier, Speichern pour sauvegarder un fichier et Beenden pour quitter le logiciel,

· Berechnungen (calculs) pour sauvegarder les données calculées dans un fichier de type texte,

· Hilfe (aide) qui ne fournit que la version et l’auteur du logiciel.

Limitations

Comme tout logiciel, Nurflügel fait des approximations dans ses calculs. Il en résulte que les ailes trop en flèche (plus de 30°) ou avec un allongement trop faible (moins de 3) ne sont pas calculées correctement. Le logiciel calculera des valeurs sans fournir d’avertissement, mais les résultats ne seront pas fiables. Les limites indiquées ici montrent en particulier qu’on ne peut pas calculer des ailes delta avec ce logiciel. Dans le cas des ailes delta ou à forte flèche, deux tourbillons (vortex) de grande amplitude se forment au saumon, ce qui confère une bonne portance à forte incidence, paramètre que Nurflügel ne sait pas prendre en compte.

Onglet introduction des valeurs (Tragflächendefinition)

Le tableau de valeurs

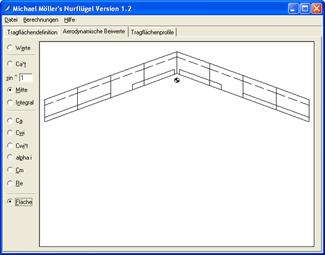
Figure 1 : Onglet d’introduction des caractéristiques de Nurflügel

            L'onglet Tragflächendefinition présenté figure 1 permet d'entrer un dessin d'ailes comportant une ou plusieurs sections (Stützstellen) linéaires avec une ou plusieurs paires de gouvernes (Klappen). Plutôt qu'un long discours, la figure 2 permet de comprendre précisément la relation entre le dessin des ailes et les cotes données (x est la coordonnée dans la direction d'avancement, y est la coordonnée perpendiculairement à l'avancement et t représente la corde).

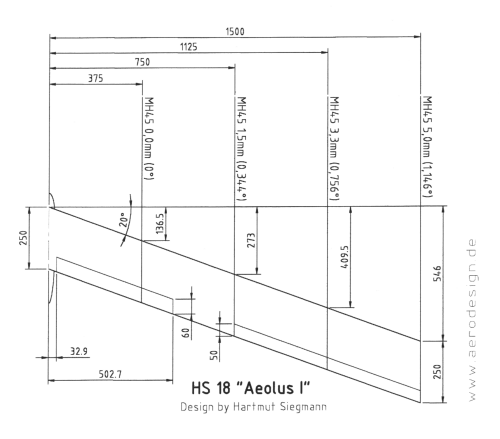
Figure 2 : Aile droite de l'Aeolus I

            Ces valeurs entrées à la main en fonction du dessin des ailes peuvent être sauvegardées (Speichern) ou récupérées (Öffnen) à partir du menu déroulant Datei en même temps que le nom du modèle (Projekt) et sa masse (Modelmasse).

Pour chaque section il faut aussi indiquer :

• l'angle de d'incidence alpha de calage de chaque section,
• l'incidence de portance nulle du profil utilisé alpha-0,
• le moment de basculement réduit Cmo à 25 % du profil,
• La portance réduite maxi du profil CaMax,
• La portance réduite maxi en vol dos du profil CaMin,
• L'angle de calage beta de chaque gouverne.

            Les valeurs qui sont fonction du profil choisi : alpha-0, Cmo à 25 %, CaMax et CaMin, pourront être obtenues par un logiciel de soufflerie numérique comme Xfoil ou JavaFoil, ou une base de données quelconque. Toutefois, alpha-0 et Cmo à 25 % peut être obtenu directement par Nurflügel en utilisant le troisième onglet Tragflächenprofile.

Attention : tous les angles sont en degrés (grad en allemand). Il ne faut pas confondre le grad allemand et le grade français (360 grad = 400 grades = 1 tour).

Boutons radio de sélection

Une fois toutes les données géométriques, aérodynamiques, ainsi que la masse entrées, il faut remplir les quatre champs à droite des boutons radio :

· position du centre de masse (Schwerpunkt),

• le taux de stabilité désiré (Stabilitätmass),
• l'incidence de vol (Anstellwinkel) ou,
• le coefficient réduit de portance moyen (Tragflächen-Ca) désiré des ailes.

Même si on ne se sert pas de certains de ces champs tout de suite, il faut les remplir avec des valeurs arbitraires aussi cohérentes que possible, car un champ vide peut empêcher les calculs ultérieurs de se faire.

Ensuite il faut sélectionner un seul de ces paramètres au choix en cochant le bouton radio correspondant.

Si on a fait un choix et introduit une valeur qui conduit à un vol stable on obtient automatiquement les trois autres valeurs dans l’onglet « Aerodynamische Beiwerte ». Dans le cas contraire (par exemple si on choisit « centre de masse » (Schwerpunkt) et une mauvaise position du centre de masse) aucun calcul ultérieur n’est fait car impossible. Dans le cas d’un modèle à empennage par nature instable pour Nurflügel qui ne prend pas en compte l’empennage, les deux seuls choix possibles sont l'incidence de vol (Anstellwinkel) ou le coefficient réduit de portance moyen (Tragflächen-Ca) retenu.

N.B. : pour être sur d'obtenir un résultat ultérieur de calcul valable de la part de Nurflügel, le mieux est de sélectionner dans un premier temps "Tragflächen-Ca" en donnant une valeur modérée, comme par exemple 0,3, valeur que l’on pourra changer par la suite.

Onglet caractéristiques aérodynamiques (Aerodynamische Beiwerte)

Pour obtenir les caractéristiques du modèle qui vient d'être entré, il suffit de sélectionner l'onglet de calcul (Aerodynamische Beiwerte) et choisir un thème à l'aide des boutons radio du bandeau de gauche. Les divers choix possibles sont dans l’ordre du haut vers le bas (voir figure 3) :

· Werte : tableau de valeurs numériques,

· Ca*t : courbe d’évolution du produit portance fois corde le long de l’aile droite comparée à la forme d’un sinus élevé à une puissance au choix,

· Courbes d’évolution de données locales le long de l’aile droite,

· Ca : courbe de portance,

· Cwi : courbe de trainée induite,

· Cwij*t : courbe du produit trainée induite fois corde,

· alphai : incidence induite par la déviation du flux d’air,

· Cm : courbe d’évolution du coefficient de moment,

· Re : courbe d’évolution du nombre de Reynolds,

· Fläche : dessin des ailes vues de dessus.

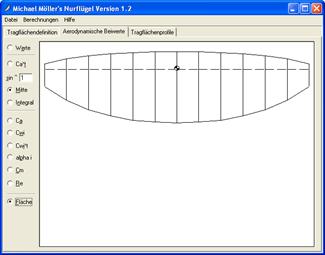
Dessin des ailes (Fläche)

           La première sélection à faire est Fläche pour obtenir et vérifier que le dessin des ailes obtenu correspond à ce qui était attendu. On peut voir sur la figure 3 le résultat des dimensions entrées à la figure 1.

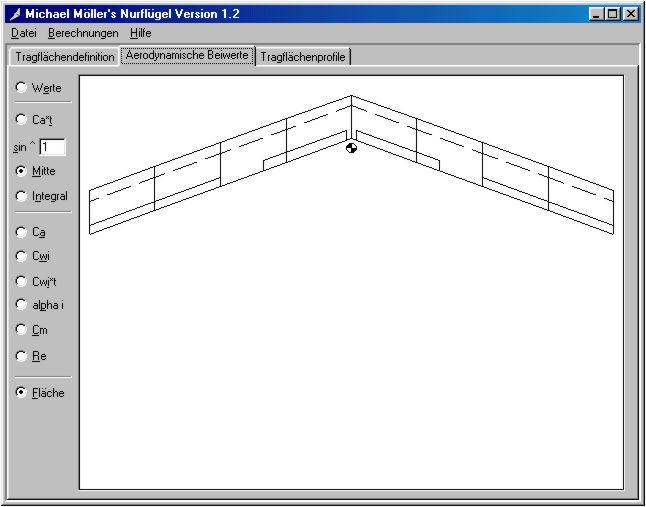
Figure 3 : surfaces portantes de l'Aeolus I

Valeurs numériques (Werte)

Les paramètres aérodynamiques principaux sont obtenus en sélectionnant les valeurs (Werte) et sont présentés à la figure 4.

Figure 4 : caractéristiques géométriques et aérodynamiques de l'Aeolus I

Les valeurs données dans l’ordre du tableau de valeurs sont les suivantes :

• la corde moyenne en décimètres Lbz,
• la position du foyer géométrique Xbz25 par rapport au bord d’attaque à l’emplanture en décimètres,
• la position du foyer aérodynamique Xnp (le vrai foyer) par rapport au bord d’attaque à l’emplanture en décimètres,
• la position du centre de masse Xdp par rapport au bord d’attaque à l’emplanture en décimètres,
• le degré de stabilité en SM en pourcentage de la corde moyenne,
• la pente du coefficient de portance dCa,
• la pente du coefficient de moment dCm,
• l'incidence de portance nulle des ailes alpha0,
• le moment réduit de basculement par rapport au foyer aérodynamique Cm0,
• le coefficient de portance réduite Ca,
• le moment réduit de basculement par rapport au foyer géométrique Cm25,
• le moment réduit de remise en ligne selon l'axe de lacet Cni,
• le coefficient de trainée induite Cwi,
• le facteur de traînée induite Cwi/cwi ell. (facteur de qualité k des ailes),
• la surface des deux ailes F en décimètres carrés,
• la charge alaire G/F en grammes par décimètre carré,
• la vitesse de vol V dans la configuration donnée dans l'onglet principal,
• l'allongement des deux ailes ST.

Courbes caractéristiques

Il est possible d'obtenir les graphes d'évolution le long de l’envergure de l'aile droite de nombreuses grandeurs importantes et secondaires en sélectionnant le bouton radio adéquat (voir plus haut). Chaque courbe importante va être décrite dans ce paragraphe dans l’ordre de présentation par Nurflügel. Afin d’expliciter la signification de chaque courbe présentée, une comparaison entre l’Aeolus, une paire d’ailes de forme rectangulaire et une paire d’aile de forme proche de l’ellipse (figure 5) va être faite ici.

Figure 5 : aile volante, ailes de forme rectangulaire et de forme quasi-elliptique qui vont être comparées

Ca*t : courbe d’évolution du produit portance fois corde le long de l’aile droite comparée à celle évoluant selon la forme d’un sinus élevé à une puissance au choix (figure 6)

Figure 6 : produit Ca*t comparé à un sinus (Aeolus, ailes rectangulaires et ailes quasi-elliptiques)

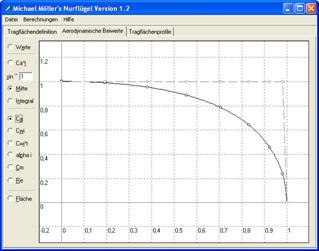
Dans l’exemple de la figure 6 on compare pour nos trois paires d’ailes l’évolution du produit Ca*t à un sinus (sinus élevé à la puissance 1). On peut remarquer que dans le cas d’ailes de forme quasi-elliptique le produit Ca*t et le sinus sont presque confondus. La courbe du produit Ca*t est surtout intéressante dans le cas de l’étude des ailes volantes de type Horten, et l’analyse sera développée dans le paragraphe correspondant.

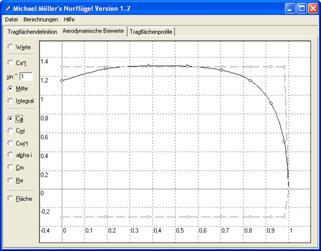
Ca : courbe de portance,

La courbe de répartition de la portance Ca (figure 7) est certainement la plus importante fournie par Nurflügel.

Figure 7 : répartition de la portance, respectivement sur l’Aeolus, des ailes rectangulaires et des ailes de forme quasi-elliptique

On observe parfaitement à la figure 7 que la portance est beaucoup mieux répartie sur les ailes de forme quasi-elliptique (à droite) que sur les deux autres. Si les ailes de droite avaient été de forme parfaitement elliptique (ce qui n’est pas le cas, notamment au saumon) le Ca aurait été strictement constant. Pour un profil ayant un Ca_Max de 1 le décrochage est à Ca = 0,83 pour des ailes rectangulaires, et à Ca = 0, 98 pour les ailes de forme quasi-elliptique.

Tout se passe comme si plus de 15 % de la surface portante était perdue dans le cas d’ailes de forme rectangulaire ; cette forme n’est donc pas idéale. Ceci étant, le décrochage commence toujours la où la charge alaire est la plus importante, donc à l’emplanture dans le cas des ailes rectangulaires, ce qui est bien pour les débutants car cela évite les départs en vrille spontanés. C’est par contre un inconvénient en acrobatie parce qu’on veut pouvoir dans ce cas partir suffisamment facilement en vrille volontaire.

Il est important de comprendre que le flux d’air incident est dévié à la fois vers le bas et vers l’extérieur (les saumons) dans le cas des ailes réelles (c'est-à-dire qui ont une envergure limitée, par opposition aux profils qui sont supposés avoir une envergure infinie). Ceci a deux conséquences :

· les ailes reçoivent un flux d’air incliné vers le bas et tout ce passe comme si leur angle d’incidence était diminué. On appelle cet angle l’angle l’incidence induit nommé alphai.

· La combinaison de déviation du flux d’air vers le bas et l’extérieur génère un tourbillon au saumon appelé vortex d’extrémité qui induit une traînée supplémentaire importante nommée traînée induite (voir chapitre aérodynamique).

Cwi : courbe de répartition de la trainée induite

Cette courbe non représentée ici est un résultat intermédiaire permettant de calculer la trainée induite globale des ailes. Elle n’est intéressante que pour le spécialiste.

Cwij*t : courbe du produit trainée induite fois corde

Cette courbe est un résultat intermédiaire comme la précédente permettant de calculer la trainée induite globale des ailes. Elle n’est aussi intéressante que pour le spécialiste.

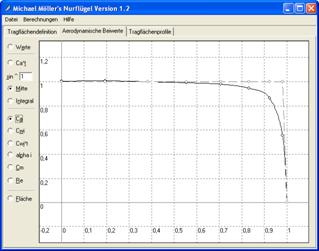
alphai : incidence induite par la déviation du flux d’air

Cette courbe présentée à la figure 8 pour nos trois cas est très importante. Elle montre comment évolue l’incidence induite alphai le long des ailes.

Figure 8 : incidence induite alphai, respectivement sur l’Aeolus, des ailes rectangulaires et des ailes de forme quasi-elliptique

Dans le cas idéal des ailes de forme elliptique, l’incidence induite alphai est constante ; c’est ce qu’on retrouve à peu de choses près avec les ailes de droite de la figure 8 ; avec dans ce cas alphai égal à environ quatre degrés. Il faudra donc augmenter l’incidence des ailes de quatre degrés pour obtenir la portance indiquée par la polaire du profil de ces ailes. Dans le cas des ailes de forme non elliptique on remarque qu’alphai augmente fortement vers le saumon. Il en résulte une portance réduite au saumon visible à la figure 7 et une perte d’efficacité globale des ailes.

Cm : courbe d’évolution du coefficient de moment

Cette courbe non représentée ici montre l’évolution du coefficient de moment Cm le long des ailes. C’est un résultat intermédiaire permettant de calculer le coefficient de moment global des ailes. Elle n’est intéressante que pour le spécialiste.

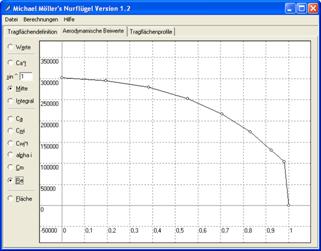
Re : évolution du nombre de Reynolds

Lorsque la corde varie, le nombre de Reynolds qui est proportionnel à la corde (voir chapitre aérodynamique) varie forcément aussi ; c’est ce qu’on peut vérifier à la figure 9.

Figure 9 : évolution du nombre de Reynolds, respectivement sur l’Aeolus, des ailes rectangulaires et des ailes de forme quasi-elliptique

Etant donné que les caractéristiques comme Ca_max et Ca_min d’un profil sont fonction du nombre de Reynolds, ces courbes permettent de rentrer des valeurs justes dans l’onglet des caractéristiques du modèle en se servant d’une soufflerie numérique comme Xfoil ou JavaFoil, ou une base de données.

Onglet profils (Tragflächenprofile)

Figure 10 : onglet Profils (tragflächenprofile) de Nurflügel

Cet onglet présenté à la figure 10 permet de visualiser des profils d’une base de données comme celle de l’UIUC [2] décrite au chapitre JavaFoil. Il permet aussi de donner quelques grandeurs géométriques comme : d (épaisseur relative), xd (position de l’épaisseur maximale), f (galbe), xf (position du maximum du galbe), et estimer quelques grandeurs aérodynamiques indépendantes de nombre de Reynolds comme : alpha0 (angle d’incidence à portance nulle), Cm0,25 (coefficient de moment au foyer géométrique), xnp (position du foyer aérodynamique), ainsi que quelques grandeurs secondaires.

Les données fournies sont utiles pour remplir certains champs de l’onglet d’introduction des données, comme pour le choix du profil. Mais comme il manque Ca_max et Ca_min fonction du nombre de Reynolds, il peut être aussi pratique d’utiliser JavaFoil pour obtenir l’ensemble des informations indispensables pour l’onglet d’introduction des données.

Si on souhaite malgré tout utiliser cet onglet pour la rapidité d’obtention des informations, il suffit de choisir dans la fenêtre de gauche le répertoire de la base de données de profils, puis le profil dans la fenêtre du centre ; on obtient alors instantanément les caractéristiques dans la fenêtre de droite et le dessin dans la fenêtre du bas.

Centrage d’un modèle

Pour qu'un aéronef soit stable dans la direction longitudinale (pas de cabrage ou de piqué spontané et retour à l’orientation initiale après une perturbation), il faut que le centre de masse soit légèrement en avant du point neutre de l'aéromodèle (voir chapitre sur la stabilité et la contrôlabilité). La distance correspondante exprimée en pourcentage de la corde moyenne Lbz des ailes est appelée marge de stabilité.

Une marge de stabilité de 5 % va bien pour un modèle moyen et un pilote ordinaire en utilisation standard. Si le modèle a des ailes hautes qui contribuent à augmenter la stabilité on pourra enlever un ou deux points de marge selon que les ailes sont moyennement hautes ou très hautes. Si on est débutant ou qu'on souhaite un modèle bien stable, au augmentera la marge d'environ deux ou trois points. Si on contraire on souhaite un modèle assez neutre pour l'acrobatie on diminuera la marge d'autant (en 3D, on peut même être amené à choisir une marge nulle). Si le modèle est très amorti (empennage de taille importante et queue longue) on pourra aussi être amené à diminuer légèrement la marge de stabilité.

Dans tous les cas, la position du centre de masse ainsi calculée sert de point de départ. On déplace ensuite au fur et à mesure des essais le centre de masse jusqu'à obtenir le comportement de l'aéromodèle le plus conforme possible à ce que l'on souhaite.

Aile volante

Dans le cas d'une aile volante, le point neutre et le foyer aérodynamique sont confondus. Il suffit donc de choisir la marge de stabilité désirée, l'indiquer à Nurflügel dans l’onglet d’entrée des données, Nurflügel fournit alors la position Xdp du centre de masse correspondante dans l’onglet des résultats.

Empennage arrière

Si l'aéromodèle a un empennage arrière (modèle classique), le point neutre est décalé en arrière du foyer aérodynamique d'une distance ka exprimée en fraction de corde moyenne définie par l'équation 1 suivante explicitée au chapitre sur la contrôlabilité et la stabilité :

ka = kα.ks.(as/aa).(Ss/Sa).(L/c) (1)

Pour trouver la position à donner au centre de masse il faut donc calculer ka et en déduire la position à donner au du centre de masse.

Exemple :

Prenons le cas du Super Miss de Scorpio qui a des ailes rectangulaires de profil Clarky et qui est défini à la figure 11. Ses ailes sont montrées à la figure 12 et le résultat des calculs de Nurflügel à la figure 13 :

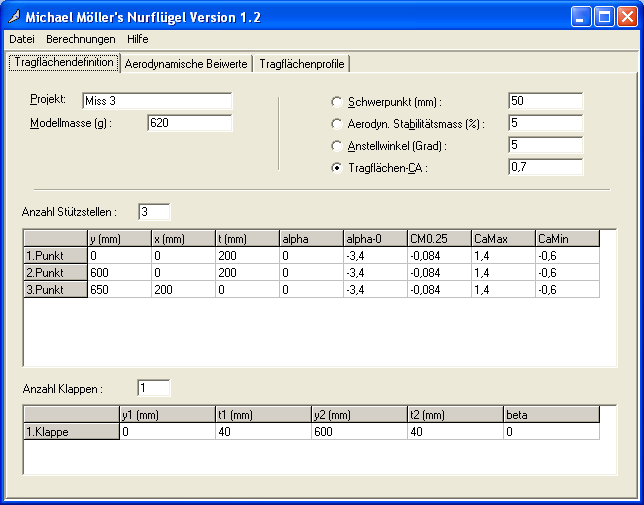
Figure 11 : géométrie du Super Miss de Scorpio

Figure 12 : ailes du Super Miss de Scorpio

Figure 13 : caractéristiques du Super Miss de Scorpio

Le coefficient ka est calculé en fonction des mesures faites sur le modèle et des coefficients choisis en fonction des critères définis au chapitre sur la stabilité et la contrôlabilité. Le tout est reporté dans la feuille de calcul centrage.xls (voir figure 14), qui se charge au demeurant de l’ensemble des calculs, comme le fera le futur le logiciel Aerocalc. Les calculs sont malgré tout détaillés ici pour le principe. On notera que dans notre cas particulier on n’a pas besoin de Nurflügel pour obtenir la corde moyenne Lbz (20 cm = 2 dm) puisqu’elle est constante, mais Nurflügel est utile dans tous les autres cas pour calculer la corde moyenne Lbz.

ka = (0,4*0,6)*(0,057/0,075)*(6,4/26,0)*(5,9/2,0) = 0,132 soit 13,2 %

Le point neutre est donc situé 13,2 % derrière le foyer aérodynamique, c'est-à-dire en recul de 0,132x20 = 2,7 cm ; la corde moyenne étant de 20 cm.

Si on prend une marge de stabilité de 5 %, on devra avancer le centre de masse de 0,05x20, soit 1 cm.

Comme Nurflügel situe le foyer aérodynamique 0,50429 dm (voir figure 13) soit 5 cm derrière le bord d’attaque, le centre de masse devra être situé à : 5 + 2,7 – 1 = 6,7 cm du bord d’attaque comme le montre le calcul et centrage.xls. On notera accessoirement que la feuille de calcul permet d’anticiper le centrage dès la conception car il suffit d’entrer la masse et la position désirée de chaque élément (moitié gauche de la figure 14) pour observer dans la case Position CM réel la position du centrage qui en résultera. On notera aussi que cette position est située à 33 % du bord d’attaque, valeur souvent adoptée en absence de tout calcul…

Figure 14 : calcul du centrage par la feuille centrage.xls assistée de Nurflügel (en vert)

Empennage canard

Si l'aéromodèle a, au contraire de la formule classique, un empennage avant, le point neutre est décalé en avant du foyer aérodynamique de la distance ka exprimée en fraction de corde moyenne définie par l'équation 1. Les calculs sont donc les mêmes avec un simple changement de signe de la distance définie par ka.

Détermination d’un aéromodèle à empennage

Profil

Le choix du profil dépend de l'utilisation envisagée de l'aéromodèle (voir chapitre sur l’aérodynamique). Il peut être affiné dans le cas de modèles de performance avec JavaFoil.

Effilement

L'effilement de l'aile permet une répartition harmonieuse de la portance réduite locale Ca. Idéalement, à la limite du décrochage, le Ca local devrait être égal au Ca_Max. La figure 7 à droite montre le cas d'une aile quasi-elliptique presque idéale par rapport à ce critère.

Néanmoins, sauf pour les modèles de performance, on ne cherche ni à donner à une aile une forme ellipsoïdale, ni même à approximer cette forme par une suite de trapèzes, car ça complique notablement la fabrication. On se contente de donner une forme approximativement trapézoïdale à chaque aile, conformément à la figure 15 qui présente les ailes d’un Artist, modèle pour l’acrobatie de Topmodel (aspect petit F3A).

Figure 15 : ailes trapézoïdales d’un modèle d’acrobatie de style F3A (Artist de Topmodel)

Avec la forme trapézoïdale de la figure 15 on arrive à la répartition de portance de la figure 16. Cette forme permet un Ca_Max global de 0,86 pour un Ca_Max de profil de 0,94. On notera que l’effilement a été délibérément limité de façon à ce que le saumon décroche après le restant de l'aile.

Figure 16 : répartition de la portance sur l’aile droite d’un Artist de Topmodel

La figure 15 montre que le décrochage commence à 45 % de l’emplanture. Ce décrochage local augmentant la charge alaire du reste des ailes provoque une rapide propagation du décrochage simultanément vers l’emplanture et le saumon. Comme la réserve de portance est supérieure au saumon, celui-ci décroche en dernier. Cette forme garantit donc un décrochage symétrique, tout en permettant un départ en vrille à l’aide d’une action énergique sur les ailerons.

Les ailes trapézoïdales, bien que moins performantes que les ailes ellipsoïdales sont de loin les plus courantes car faciles à fabriquer. Le tout est de choisir le degré d'effilement. Tant que la corde au saumon dépasse la moitié de la corde à l'emplanture il n'y a guère de problème ; au-delà, les départs en vrille risquent d'être brutaux. Un effilement d'un tiers seulement conduit à un comportement très sain, et c'est une valeur couramment retenue, sauf pour les planeurs pour lesquels les ailes doivent être mieux optimisées.

Flèche

Il y a quatre raisons pour donner une flèche aux ailes d'un aéronef :

• augmenter le nombre de Mach critique, mais ça ne concerne guère nos aéromodèles,
• augmenter l'amortissement longitudinal, ce qui est souvent nécessaire dans le cas d'utilisation d'un empennage canard,
• augmenter la stabilité en lacet, ce qui est utile si l'empennage vertical est trop petit ou absent,
• rendre des ailes auto-stables sans utiliser de profil auto-stable en vrillant en plus les extrémités des ailes (cas des ailes volantes de type Horten décrites plus loin dans ce chapitre).

Vrillage

Une alternative à la forme ellipsoïdale pour obtenir une bonne répartition du Ca en conservant une forme trapézoïdale (ou autre forme non optimale), est de vriller les ailes. En l'occurrence cela revient dans le cas d'ailes trapézoïdales à augmenter l'incidence à l'emplanture.

Cette technique est largement utilisée dans l'aviation de transport car elle est surtout efficace dans le cas d'une faible plage de vitesses. Or les avions de transport ont justement une très faible plage de vitesse. Typiquement leur vitesse aérodynamique est presque fixe et d'environ 450 km/h (selon la charge : passager + fret + kérozène). Lorsqu'ils sont à haute altitude la vitesse réelle est double, mais la vitesse aérodynamique n'augmente pas du fait de la raréfaction de l'air. Au décollage et à l'atterrissage, la vitesse n'est plus faible qu'en raison de l'utilisation de volets à fentes et de becs de bords d'attaque. Ceci explique pourquoi les ailes des avions de transport sont optimales bien qu’elles ne soient pas ellipsoïdales.

Détermination d’une aile volante de type Fauvel

Profil

Charles Fauvel [4] a choisi un profil auto-stable pour ses ailes volantes. Ce profil est présenté à la figure 17 ci-après.

Figure 17 : profil auto stable Fauvel

Comme on peut le remarquer, la courbure est réflexe, c'est-à-dire normale à l’avant et inverse à l’arrière. Certains auteurs parlent de courbure en S. On trouve ce type de profil assez souvent aussi sur les ailes delta. Pour conserver une portance suffisante l’épaisseur relative est importante (14%). L’inconvénient est une finesse limitée, fait d’autant plus significatif que Fauvel utilisait ce profil pour des planeurs.

Effilement et flèche

Pour une bonne utilisation du profil, un effilement important (de l’ordre de 50 %) est retenu. La figure 18 présente une PicoJet de Muliplex, aile volante de type Fauvel typique.

Figure 18 : ailes d’une aile volante PicoJet de Multiplex de type Fauvel

Comme le profil est auto-stable et l’allongement limité, l’utilisation d’une flèche est inutile.

La figure 19 montre que la répartition de portance est bonne du fait de l’effilement important. Par contre, cette répartition peut être à l’origine de départs en vrille imprévus (non observés à l’ usage) ; contrepartie de la bonne utilisation de la surface portante. Dans notre exemple le profil Fauvel avec un Ca_Max de 1,05 permet un Ca_Max d'aile de 0,97 ce qui est très correct.

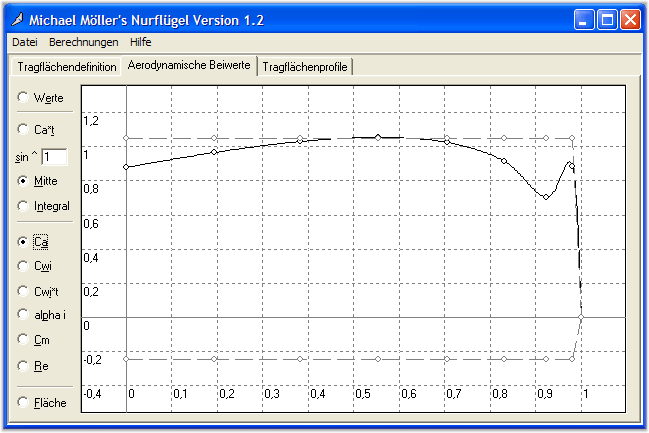
Figure 19 : distribution du Ca sur les ailes de la figure 18

Détermination d’une aile volante de type Horten

Profil

Comme il n'y a pas d'empennage, les ailes volantes doivent être intrinsèquement stables, ce qui peut être obtenu soit avec un profil auto-stable comme cela vient d’être montré au paragraphe précédant, soit à partir d'un profil classique mais en utilisant une forte flèche et en vrillant les ailes de façon à diminuer l'incidence aux saumons. Cette seconde technique est celle qui a été retenue par les frères Horten [5] en Allemagne durant le second conflit mondial. Ils utilisaient typiquement un profil peu galbé.

Effilement, flèche et vrillage

Les ailes volantes de type Horten n’ont pas d’empennage vertical (on parle parfois d’aile volantes pures) car la forte flèche (voir figure 20) et le vrillage négatif (voir figure 21) utilisés pour la stabilité en tangage permettent aussi d’obtenir la stabilité en lacet. De plus, du fait du vrillage négatif l’incidence reste très faible au saumon, ce qui limite le lacet inverse qu'on ne pourrait pas contrer faute d'empennage vertical.

Figure 20 : aile volante pure de type Horten

On remarquera à la figure 20 la flèche associée au fort effilement typique. La corde à l'emplanture est ici aussi augmentée comme sur les avions de ligne, ce qui n'est pas nécessaire mais simplifie l'optimisation.

Figure 21 : géométrie de l'aile Horten de la figure 20. Remarquer le vrillage colonne alpha-0

La figure 21 permet de bien appréhender les détails de conception de l'aile volante de la figure 20.

Il faut remarquer en particulier :

• le vrillage négatif qui augmente à partir de la troisième section (le vrillage de la première section ayant été évité en augmentant la corde à l'emplanture),
• le profil utilisé strictement neutre (Cm_0,25 = 0),
• le Ca_Max qui diminue vers le saumon, conséquence de l'effilement qui diminue le nombre de Reynolds et donc l'efficacité du profil vers le saumon,
• le Ca nominal faible retenu de 0,3.

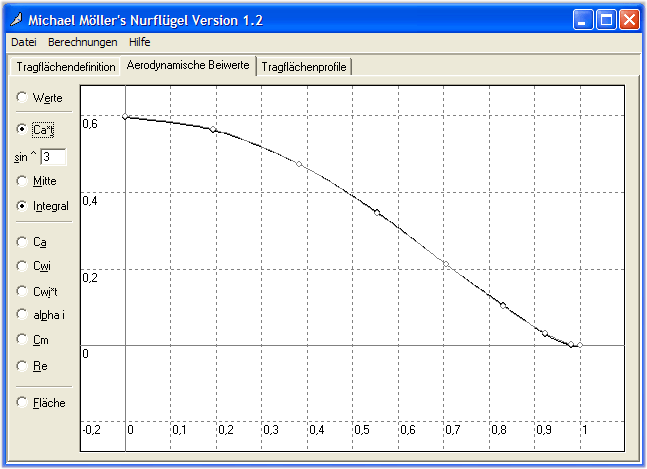
Figure 22 : Evolution du produit Ca*t selon la forme d'une cloche (sin³)

La technique la plus classique de réglage du vrillage consiste à faire suivre au produit Ca*t la forme d’une cloche (cube d'une fonction sinus). La figure 22 démontre la technique. Malheureusement dans ce cas, la surface externe de l'aile est imparfaitement utilisée, comme le montre la figure 23. C'est la contrepartie de cette technique.

Figure 23 : évolution de la portance le long de l'aile volante de la figure 20

La figure 24, dernière de ce chapitre, montre l’évolution du Cm local de l’aile volante de la figure 20 et met bien en évidence le comportement déstabilisant de la surface proche de l’emplanture, plus que compensée par la large zone stabilisante proche du saumon, permettant d’obtenir un Cm positif global suffisant.

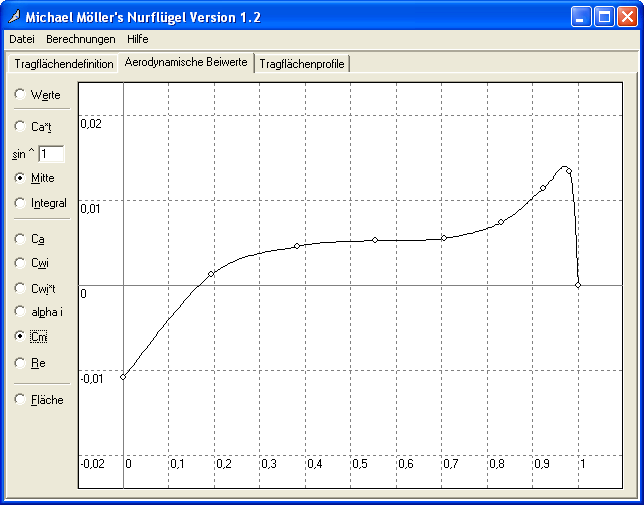
Figure 24 : moment local de tangage généré par la flèche et le vrillage de l’aile volante Horten de la figure 20

Références

1. Manuel et téléchargement de Nurflügel version 1.2 (site Aerodesign)
2. Base de données de profils de l’UIUC
3. Version 2.26 de Nurflügel (site Zanonia)
4. Biographie de Charles Fauvel
5. Biographie des Frères Horten (site Aerostories)