Aéromodélisme RC

Techniques et conception

Les matériaux de construction

Lien vers « Sauver un animal »

Sommaire général

Auteur : Philippe Kauffmann

Version initiale : 2008

Dernière révision : 8 juillet 2014

Photos : constructeur ou auteur, sauf mention contraire

N. B. : double-cliquer sur les images permet souvent d’obtenir une version agrandie.

Sommaire

Les efforts et contraintes mécaniques

Efforts principaux dans un avion grandeur

Efforts principaux dans un aéromodèle

Résistance et déformation des matériaux aux efforts

Les caractéristiques générales des matériaux

La traction, la compression, le flambage et le déversement

La flexion

Ailes

Clef d’aile

Mesure de la contrainte maximale acceptable par un matériau

La torsion et l’aéroélasticité

La concentration de contrainte

Caractéristiques mécaniques des principaux matériaux de construction

Matériaux classiques

Autres matériaux

L’ABS

Le carton

Les matériaux expansés

Les matériaux extrudés

Avantage des matériaux à faible densité

Références

Le bon choix du matériau de construction, tout comme la manière de l’utiliser, sont essentiels pour un aéromodèle, car c’est ce qui va déterminer sa masse, donc son domaine de vol, tout comme sa capacité à résister aux efforts subis par le vol. Un matériau mal choisi ou mal mis en œuvre alourdit inutilement un modèle ou le fragilise. L’intuition dans ce domaine est souvent mauvaise conseillère car, par exemple, un renforcement excessif au mauvais endroit va alourdir le modèle, et en augmentant de ce fait les efforts, va finalement le fragiliser au lieu de le renforcer.

Les efforts et contraintes mécaniques

Avant toute chose il convient de définir les notions d’effort et de contrainte.

Supposons qu’on dispose d’un fil vertical d’une section circulaire de 1 mm² attaché par le haut et qu’on y suspende une masse d’un kg. Le fil subit alors une force de traction nommée effort d’un kgf (kilogramme force). Le kilogramme force n’étant une unité fondamentale du Système International, on utilise en général plutôt le Newton noté N. Le Newton étant 9,81 fois plus petit que le kgf, notre fil supporte donc un effort de 9,81 N.

Etant donné que la résistance d’un fil est proportionnelle à sa section, on préfère bien souvent utiliser la notion de contrainte qui est l’effort divisé par la section du fil et qui est en général représentée par la lettre grecque s. Ainsi, notre fil subira une contrainte s de 9,81 N/mm². Lorsqu’on choisira un fil, on prendra une section telle que la contrainte ne dépasse pas la contrainte maximale admissible par le matériau du fil, valeur connue pour tout matériau classique.

Efforts principaux dans un avion grandeur

Lorsqu’un avion vole en ligne droite à vitesse constante il subit une charge de 1 G, c'est-à-dire une fois la gravité terrestre, donc son poids. A la conception de l’avion, les ingénieurs calculent dans ces conditions en fonction de la charge utile et du poids de chaque élément de l’avion, la contrainte subie par chaque élément de l’avion.

Lorsqu’un avion effectue un virage ou une ressource, il supporte une charge supérieure. Par exemple, lors d’un virage incliné à 45° la charge subie est de 1,4 G. La charge maximale que l’avion est susceptible de subir est déterminée par la portance des ailes à la limite du décrochage (voir chapitre : domaine de vol des aéromodèles). Typiquement on calcule les avions pour qu’ils puissent résister à une charge maximale de 4 G (avion civil) à 10 G (avion de combat). La charge maximale qu’un avion est susceptible de subir étant proportionnelle au carré du rapport de la vitesse de l’avion sur sa vitesse de décrochage, un avion calculé à 4 G et décrochant à 300 km/h ne devra jamais dépasser 300xÖ4 = 600 km/h (valeur typique pour un avion de transport à faible altitude). Chaque pièce est donc dimensionnée pour ne pas subir dans ces conditions une contrainte s supérieure à celle que le matériau peut accepter.

La zone où l’effort est le plus important dans un avion en vol est à la jonction des ailes avec le fuselage, car tout le poids du fuselage se reporte en cet endroit sur les ailes.

L’effort sur le train d’atterrissage au moment du contact est également très important. Le principe général sur un avion grandeur est que le train principal doit pouvoir supporter un atterrissage selon une pente et une vitesse normale sans arrondi.

Tous les blocs d’alliage d’aluminium utilisés pour fabriquer les pièces d’avion sont vérifiés à la sortie du laminoir aux ultrasons et au détecteur rhéologique par des contrôleurs assermentés indépendants, avant de subir un test de traction à la contrainte s_max.

N. B. : la majorité des blocs d’alliage d’aluminium pour les Airbus sortent de l’usine ALCAN d’Issoire (Issoire, siège des 5A) où sont élaborées des tôles fortes pouvant atteindre 0,3x2x30 m de dimensions principales.

Efforts principaux dans un aéromodèle

Nos aéromodèles répondent aux mêmes lois physiques que les avions grandeur, mais il faut ajouter les chocs sur les bords d’attaque et les saumons, sur l’avant de l’avion (moteur) et l’écrasement des éléments (en particulier du fuselage) par les manipulations ; efforts qui peuvent devenir prédominants…

La grande différence avec les avions grandeur est qu’on est en général incapable de calculer les contraintes sur la plus grande partie de l’aéromodèle. Néanmoins, il est possible, sinon souhaitable, de calculer les efforts aux endroits critiques, surtout s’il s’agit d’un modèle pouvant voler vite, car il ne faut pas perdre de vue qu’un modèle de 2 kg volant à quatre fois sa vitesse de décrochage peut subir 16 G et que dans ces conditions ses ailes devront être capables d’encaisser plus de 30 kg sans broncher.

Il est donc utile de calculer la résistance des ailes et la clef de montage si le modèle en est pourvu. Aerocalc étant au demeurant prévu pour effectuer ce calcul dans une version ultérieure. Pour le reste, la solidité est définie par la technique de construction et est en général suffisante si on utilise les matériaux adéquats placés aux bons endroits.

Résistance et déformation des matériaux aux efforts

Les caractéristiques générales des matériaux

Lorsqu’un effort et donc une contrainte est appliquée sur un matériau il se déforme. Typiquement, si on applique un effort croissant sur une barre de matériau quelconque, elle s’allonge d’abord proportionnellement avec cet effort, puis finit par se rompre. La figure 1 donne les courbes type de déformation jusqu’à la rupture pour les deux types de matériaux courants, ceux dits ductiles et ceux dits fragiles.

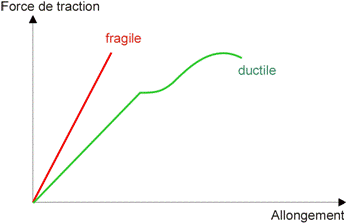
Figure 1 : allongement à la traction d’un matériau ductile et fragile

Dans le cas d’un matériau fragile (courbe rouge), les choses sont simples : l’allongement est strictement proportionnel à l’effort. Si on relâche à n’importe quel moment l’effort, le matériau reprend sa forme d’origine. Si on atteint la limite de rupture, le matériau se brise sans prévenir.

Dans le cas d’un matériau ductile (courbe en vert), le comportement est le même jusqu’à une limite appelée limite élastique. A ce point précis, le matériau se distend subitement sans effort supplémentaire, puis continue de s’allonger avec l’effort mais de façon non linéaire jusqu’à la rupture. Si on relâche l’effort dans cette zone, le matériau ne revient pas à sa forme initiale, il a subi une déformation plastique irréversible.

Les anciens ont utilisé les matériaux ductiles comme le bronze et le fer dès leur découverte car ils appréciaient énormément le fait qu’ils ne cassent pas sans prévenir comme la pierre et acceptent des déformations plastiques considérables ; la déformation par forgeage étant devenue au demeurant une technique de façonnage privilégiée. Les premiers aviateurs ont aussi apprécié l’aluminium des ailes qui ployait quand on poussait l’avion un peu trop loin sans se rompre comme le bois.

Les matériaux ductiles sont typiquement les métaux. Les matériaux fragiles sont les fibres de verre, de carbone, et le bois.

Si on distingue les matériaux ductiles des matériaux fragiles, on distingue aussi les matériaux selon qu’ils sont isotropes ou anisotropes. Un matériau isotrope est un matériau qui se comporte de la même façon aux efforts dans les trois directions de l’espace. Un matériau anisotrope est un matériau qui se comporte mieux dans une ou deux directions privilégiées.

· Les métaux sont typiquement isotropes, ce qui est bien utile lorsque les contraintes peuvent venir de plusieurs directions.

· Un jonc de carbone ou une planche de bois sont unidirectionnels. Ils ne résistent correctement que dans la direction des fibres.

· Une feuille de composite tissée ainsi qu’une planche de contreplaqué ont des fibres croisées. Ce sont donc des matériaux bidirectionnels. Ils résistent bien tant que les efforts restent dans le plan de la feuille du matériau.

Selon le contexte : efforts dans une deux ou trois directions, on sera donc amené à privilégier un matériau unidirectionnel, bidirectionnel ou isotrope.

Il y a deux autres propriétés des matériaux qui nous concernent moins, mais méritent tout de même d’être évoquées :

· La fatigue qui est la fragilisation progressive d’un matériau suite à des efforts alternatifs répétés comme par exemple la compression et décompression de l’habitacle d’un avion (des centaines de passagers d’avions de ligne sont morts à cause de la fatigue mal maîtrisée des alliages d’aluminium).

· Le fluage qui est la déformation lente, progressive et irréversible sous l’effort. Dans un moteur à explosion bien conçu à chemise fonte et piston acier, la chemise s’use et voit donc son diamètre augmenter avec le temps, en même temps que le diamètre du piston augmente sous l’effet de tassement lié au fluage induit par la pression des gaz ; ce qui rend le moteur presque inusable (c’était un des arguments de vente du fabricant ROSSI).

La traction, la compression, le flambage et le déversement

La traction

On distingue plusieurs types d’efforts. Le plus simple et qui sert de référence pour les autres cas est l’effort de traction. Pour tout calcul, il est essentiel de connaître la résistance maximum à la traction élastique (ou à la rupture dans le cas de matériaux fragiles) de tous les matériaux qu’on utilise. Dans le cas des matériaux peu résistants, la mesure peut se faire directement en tirant sur une éprouvette de test comme le montre la photo 1. Sur cette photo on a testé la résistance d’un morceau polystyrène extrudé (variante de Dépron) de 3 x 3mm de section qui a rompu à environ 900 g. L’effort maximal acceptable est donc dans ce cas de 0,9x9,81 = 8,8 Newton. La contrainte maximale à la rupture de notre matériau est donc σ_max ≈ 9/3x3 = 1 N/mm².

On parle aussi parfois de contrainte maximale spécifique τ, qui est la contrainte maximale divisée par la densité du matériau. Dans notre cas la on a τ = 1/0,03 = 33 N/mm². La contrainte maximale spécifique d’un bon acier, à titre de comparaison, est d’environ 140 N/mm². L’acier est donc, rapporté à la densité et la résistance mécanique, plus léger que le Dépron. La contrainte maximale spécifique est utile pour comparer des matériaux de densité différente car elle indique la capacité d’une certaine masse de matériau à résister à un effort donné. C’est aussi une bonne mesure de résistance pour les matériaux à densité fluctuante comme le bois et le polystyrène extrudé ou expansé car leur contrainte maximale spécifique varie beaucoup moins que leur contrainte maximale.

Par exemple : un balsa de densité 0,07 sera typiquement trois fois moins résistant qu’un balsa de densité 0,21, ce qui est assez logique.

Photo 1 : essai en traction d’un échantillon de polystyrène extrudé

Lorsqu’on tire sur une tige homogène, l’allongement observé est proportionnel à l’effort de traction appliqué. La relation a été exprimée la première fois en 1678 et en latin par Robert Hooke [1] : ut tensio sic vis. Ceci se traduit mathématiquement par l’équation 1 ci-après :

s = E.e (1)

Dans cette équation s est bien sûr la contrainte, E représente le module d’élasticité de Young [2] (même unité que la contrainte) et e l’allongement relatif sans unité exprimé par l’équation 2 :

e = (l – lo)/lo (2)

Dans l’équation 2, lo est la longueur de la tige au repos et l la longueur de la tige sous la contrainte.

E est parfois aussi appelé raideur, car plus E est grand, plus l’allongement est faible. On exprime couramment ce module de Young, spécifique de chaque matériau, en N/mm², mais le GPa est aussi souvent utilisé (1 GPa = 1000 N/mm²). La valeur de E tourne autour de 10000 N/mm² pour le bois. Ceci signifie qu’une baguette de pin sous une contrainte de traction s de 100 N/mm² (limite typique de rupture) s’allonge e = s/E = 1/100 = 0,01, c'est-à-dire de 1 %, soit de 1 mm pour une baguette de 1 m de longueur.

Compression, flambage et déversement

L’effort complémentaire de la traction est la compression. La majorité des matériaux se comportent en compression à peu près comme en traction, mais ce n’est pas toujours le cas. Le béton, par exemple, se comporte très bien en compression mais très mal en traction ; d’où les bétons armés et précontraints dans lesquels des barres de fer ou tiges d’acier subissent la traction à la place du béton. Le béton flue aussi beaucoup les premiers jours après la coulée. Il faudra en tenir compte si vous souhaitez faire des parties de modèle réduit en béton !

Une tige carrée dont la longueur est inférieure à dix fois le coté pourra être comprimée, mais si la longueur relative augmente elle aura tendance à se courber au lieu d’accepter la compression. On parle alors de flambage. Il faut absolument éviter le flambage, ce qui oblige à limiter la longueur de tous les éléments travaillant en compression, d’où les treillis si célèbres de Gustave Eiffel, mais aussi ceux des fuselages de nombreux avions un peu anciens. Calculer la longueur maximale d’une tige et la « déprécier » pour tenir compte du flambage est délicat. On se contera en modélisme d’expérimenter. On prend une tige et on tente de la comprimer. Si elle se galbe c’est qu’elle est trop longue !

Il y a pire que le flambage : le déversement. C’est le vrillage supplémentaire d’une tige longue durant le flambage.

La flexion

La traction résulte typiquement d’un effort appliqué dans la direction principale de la pièce considérée (typiquement une tige, une baguette ou un tube, nommés poutre en mécanique). A la différence de la traction, la flexion résulte typiquement d’un effort perpendiculaire à la direction principale de la poutre et appliqué à l’extrémité ou sur toute la longueur de cette poutre. C’est le type d’effort que subissent notamment les ailes et les clefs d’aile.

Dans le cas des ailes, on peut considérer qu’il s’agit d’une compression du longeron supérieur combinée à une traction du longeron inférieur suite au moment flexion de l’aile induit par la portance.

La figure 2 montre un exemple simplifié où deux longerons de longueur L séparés d’une distance constante e résistent à un effort F appliqué dans la direction perpendiculaire à la direction principale des deux longerons au bout de la structure.

Figure 2 : flexion sur une structure à deux longerons

La force en bout d’aile de longueur L se traduit par un moment M existant tout au long de la structure et qui augmente linéairement de l’extrémité droite de la structure jusqu’au début de celle-ci selon l’équation 3.

M = F.(L – l) (3)

Pour contrer ce moment, chaque section de structure présente, selon le 3^ème principe de Newton [3], un moment égal et opposé. De fait, le longeron supérieur subit un effort de compression f, tandis le longeron inférieur subit une traction f égale et de valeur :

f.e = M (4)

En combinant les équations 3 et 4 on obtient les efforts de traction et compression f le long de chaque longeron (équation 4).

f = F.(L –l)/e (5)

L’équation 5 montre que plus on s’éloigne du point d’application de la force F, plus les efforts sur les longerons augmentent. Des ailes devront donc être plus résistantes au niveau du fuselage qu’à l’extrémité. Aussi, plus on écarte les longerons, moins les efforts sont importants, d’où les ailes très épaisses (jusqu’à 22 % à l’emplanture) des avions de la seconde guerre mondiale. C’est aussi cette analyse qui a conduit les pionniers à faire des biplans avec des ailes minces très éloignées l’une de l’autre, reliées par un treillis. Les ailes du bas travaillaient en traction, celles du haut en compression et les efforts étaient minimisés par l’énorme distance entre les ailes.

Mais en pratique pour que ça marche, il faut empêcher le longeron supérieur de flamber, d’où la nécessité de placer de nombreuses nervures pour empêcher le flambage des deux longerons, ou une planchette d’écartement à fibres verticales (l’effort étant perpendiculaire à celui dans les longerons).

Ailes

Le cas d’une aile réelle est plus complexe que le cas qui vient d’être présenté car l’effort de portance, à peu près proportionnel à la surface, est réparti tout au long des ailes. Ce calcul est un peu compliqué à mener à la main, raison pour laquelle Aerocalc s’en chargera dans une version ultérieure. En attendant, la feuille de calcul jointe flexion.xls permet de faire ce calcul dans le cas d’une aile trapézoïdale non vrillée. L’exemple présenté à la figure 3 montre les courbes de portance et contrainte dans les longerons de notre « mini F3A » de référence à partir de ses dimensions, charge alaire nominale et accélération maximale.

On remarque que le moment de flexion augmente vers l’emplanture, ce qui est logique, mais on remarque aussi que l’effort dans les longerons est maximal à environ 25 % de l’envergure. Cet effort maximal dépasse 900 Newtons, ce qui est considérable. Les longerons devront donc être suffisamment dimensionnés. On peut éventuellement se passer de calculer les longerons pour un modèle ordinaire, mais pas dans le cas de modèles très sollicités ; à moins de prendre des risques…

Dans le cas de notre « mini F3A » de référence, si on utilise des longerons en pin pouvant supporter une contrainte maximale σ_max = 100 N/mm² et qu’on prend un coefficient de sécurité de 3 pour tenir compte de l’hétérogénéité du matériau et des concentrations locales de contrainte (voir plus loin), il faudra prendre des longerons de section minimale : 3x930/100 = 30 mm². Des longerons de section 4x8 mm (soit 32 mm²) feront l’affaire.

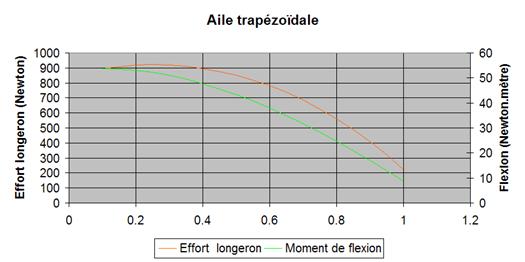
Figure 3 : répartition des efforts sur une aile trapézoïdale

Le problème qui vient d’être traité est celui d’une poutre constituée de deux longerons supposés de dimension négligeable par rapport à leur distance de séparation. Ce cas de figure correspond aussi aux poutres de section en forme de I tant utilisées en génie civil. Si on considère une poutre qui ne peut pas être réduite à deux éléments de petite taille suffisamment éloignés, les calculs se compliquent car les contraintes ne peuvent plus être supposées comme constantes à l’intérieur des éléments de la poutre.

Dans le cas d’une poutre pleine rectangulaire, la contrainte varie linéairement à l’intérieur de la section de la poutre (comme le plus souvent). Elle est nulle au centre et maximale à l’extérieur comme le montre la figure 4.

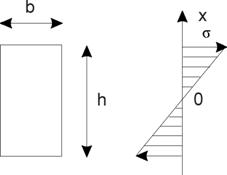
Figure 4 : répartition des contraintes dans la section d’une poutre rectangulaire

La contrainte σ dans une poutre rectangulaire peut se déduire en fonction du moment subi M et de la distance verticale z par rapport au centre de la section à l’aide de l’équation 6 :

(6)

On a l’habitude de présenter l’équation 6 sous la forme plus condensée et générale de l’équation 7, dans laquelle on a remplacé b.h³/12 par I. La terme I est appelé inertie quadratique car sa grandeur physique est une longueur à la puissance 4.

(7)

Pour que l’équation 7 reste valable quelle que soit la forme de la section de la poutre, I a une équation variable, fonction des dimensions et de la forme de la poutre. Le tableau 3 donne les inerties quadratiques des poutres de forme classique qui nous concernent :

Forme	Inertie
Rectangle
Tube rectangulaire
Rond
Tube rond

Tableau 3 : inertie quadratique de quelques poutres

L’effort de flexion provoque des déformations beaucoup plus notables que l’effort de traction. Il n’est pas exceptionnel d’observer les bouts d’ailes d’un avion de ligne fléchir de plus d’un mètre au saumon au moment du décollage. Cette déformation est, comme la contrainte, fonction du moment M et de l’inertie quadratique de la section considérée.

On peut facilement obtenir la déformation d’une poutre en flexion à partir l’équation 8 de la courbure locale g en un point x :

(8)

La courbure g en un point x de la poutre est l’inverse du rayon du cercle tangent en ce point de la poutre. Tant que la déformation reste faible, c’est la dérivée seconde du déplacement vertical z de la poutre au point x considéré. Il suffit donc d’intégrer deux fois l’équation 8 en tenant compte des conditions aux limites pour trouver la déformation en tout point de la poutre. Le calcul fait donc appel au calcul infinitésimal introduit par Newton à qui on doit décidément beaucoup plus qu’une recette de tarte aux pommes. Comme tout le monde ne pratique pas cette technique de calcul Aerocalc se chargera dans une version ultérieure aussi des calculs de déformation pour nous.

Clef d’aile

L’élément le plus sollicité dans un aéromodèle étant la clef d’aile, si on ne calcule qu’un élément dans son modèle, c’est celui-la qu’il faut choisir. Trop forte le poids de la clef pénalise le modèle, trop faible…

Prenons comme d’habitude le cas de notre « mini F3A » de référence. Soit une clef d’aile en tube Dural (σ_max = 350 N/mm²) dans un fourreau en fibre de verre (σ_max = 450 N/mm²). Le moment M à l’emplanture est égal 54 N.m d’après la figure 3. Si on prend un ensemble clef/fourreau tubulaire de 20 mm de diamètre et 1 mm d’épaisseur on aura d’après l’équation 7 et le tableau 3 :

, ce qui est limite acceptable (coefficient de sécurité inférieur à 2) puisque le σ_max du Dural est de 350 N/mm². Etant donné que le fourreau est plus résistant que la clef (σ_max = 450 N/mm²), il est inutile de le calculer.

Mesure de la contrainte maximale acceptable par un matériau

L’utilisation de la flexion d’une poutre rectangulaire (une planche peut être assimilée à une poutre) est aussi très utile pour calculer la contrainte maximale acceptable par un matériau. Dans l’industrie on utilise des machines de traction, mais pour le modéliste moyen la flexion est un excellent substitut qui ne demande que très peu de matériel. La figure 5 montre la mesure de la contrainte maximale acceptable par une baguette.

Figure 5 : mesure de la résistance maximale à la flexion d’une baguette

La méthode consiste à appliquer un moment connu à une poutre (baguette ou planchette) en pendant un objet de masse connue et en augmentant progressivement la longueur L suspendue jusqu’à la limite élastique ou la rupture. La longueur L à la rupture ou au début de la déformation plastique permet de connaître la contrainte maximale grâce à la formule 9 déduite de l’équation 6. La méthode n’est pas strictement rigoureuse car on a négligé l’effort de cisaillement et la concentration de contraintes à l’encastrement, mais elle est suffisante dans le cadre du modélisme. C’est une méthode privilégiée en modélisme pour tester les matériaux de construction car elle implique des forces beaucoup plus faibles que les essais de traction que nous ne pouvons utiliser que pour des matériaux très peu résistants (matériaux expansés).

(9)

Mesurons par exemple la contrainte maximale à la rupture d’une baguette de balsa de 6x6 mm et densité 0,17. L’expérience montre qu’elle rompt lorsqu’une masse m de 870 g est placée à L = 118 mm, ce qui correspond à :

Ceci correspond à une contrainte maximale spécifique de 165 N/mm² du fait de la densité de 0,17. On remarquera que cette valeur est bien meilleure que celle du Dépron, et même meilleure que celle de l’acier (voir tableau des caractéristiques des matériaux plus loin). Le balsa est donc un excellent matériau de construction.

La torsion et l’aéroélasticité

Un autre type d’effort couramment rencontré est l’effort de torsion qu’on utilise dans les ressorts, mais qu’on retrouve aussi dans les ailes. En effet une aile subit aussi un effort en torsion car la portance ne passe pas, sauf exception, par le centre d’inertie de l’aile. Selon que le centre d’inertie est en avant ou en arrière de la portance, l’aile ne posera pas, ou au contraire posera des problèmes d’aéroélasticité (oscillations entretenues). On a un problème d’aéroélasticité lorsque la portance entraîne un vrillage qui augmente l’incidence et donc la portance ; l’aile peut alors se mettre à vibrer dangereusement. Ce problème est accentué dans le cas des ailes en flèche inverse, c’est pourquoi on ne les aime pas beaucoup malgré leurs qualités aérodynamiques.

La concentration de contrainte

On voit dans la figure 4 la contrainte évoluer progressivement dans la section de la poutre. Ceci est lié au fait que la déformation (compression ou extension) est elle-même progressive. Lorsqu’on utilise des pièces dont la section varie brutalement, la surépaisseur locale limite la déformation, ce qui induit à cet endroit une diminution de la contrainte. Comme l’effort global subi ne change pas, une diminution locale de la contrainte implique une augmentation vers le reste de la pièce, donc une concentration de contrainte dans la zone la plus éloignée de la variation brutale de section.

L’augmentation de contrainte due à une concentration de contrainte peut conduire localement au dépassement de la contrainte de rupture, ce qui induit une micro-fissure à cet endroit. Cette micro-fissure (nommée à juste titre une amorce de rupture) augmente encore la concentration de contrainte par diminution de la section travaillante, et on arrive finalement par effet boule de neige à une rupture complète de la pièce impliquée. Plusieurs centaines de passagers d’avions de ligne doivent leur mort à une sous-estimation de ce phénomène par les ingénieurs.

En ce qui nous concerne, cela signifie que toutes les découpes doivent se faire avec des arrondis généreux, qu’il ne faut jamais augmenter brutalement une section (en collant par exemple ponctuellement une baguette sur une autre pour augmenter localement sa résistance sans faire de découpe d’extrémité en biseau accentué). Cela signifie aussi qu’il faut surveiller l’apparition des fissures génératrices de concentrations de contraintes, signes avant coureurs de catastrophe.

Caractéristiques mécaniques des principaux matériaux de construction

Matériaux classiques

Il est évident que pour la construction d’un modèle on aura intérêt à choisir un matériau dont la contrainte maximale spécifique à la rupture est la plus élevée possible. Le tableau 4 ci-après permet de comparer les matériaux les plus courants utilisés dans notre hobby.

Nature	Type	Plage de densité	E typique	smax typique	τmax typique
Balsa	Unidirectionnel	0,07 à 0,21	3500 N/mm^2	22 N/mm^2	160 N/mm^2
Samba	Unidirectionnel	0,2 à 0,4	7000 N/mm^2	55 N/mm^2	180 N/mm^2
Pin	Unidirectionnel	0,4 à 0,6	10000 N/mm^2	100 N/mm^2	200 N/mm^2
Contreplaqué hêtre	Bidirectionnel	0,7 à 0,8	12500 N/mm^2	80 N/mm^2	110 N/mm^2
Fer	Isotrope	7,8	196000 N/mm^2	230 N/mm^2	30 N/mm^2
Corde à piano	Isotrope	7,8	220000 N/mm^2	1100 N/mm^2	140 N/mm^2
Alu ménager	Isotrope	2,7	69000 N/mm^2	55 N/mm^2	20 N/mm^2
Dural	Isotrope	2,7	75000 N/mm^2	350 N/mm^2	130 N/mm^2
Composite verre	Bidirectionnel	2	30000 N/mm^2	450 N/mm^2	220 N/mm^2
Composite aramide	Bidirectionnel	1,4	45000 N/mm^2	530 N/mm^2	380 N/mm^2
Composite carbone	Bidirectionnel	1,6	88000 N/mm^2	560 N/mm^2	350 N/mm^2
Composite carbone	Unidirectionnel	1,55	200000 N/mm^2	1250 N/mm^2	800 N/mm^2

Tableau 4 : caractéristiques typiques des principaux matériaux de construction

Le tableau 4 nous montre que les meilleurs matériaux ne sont pas forcément ceux qu’on croit. Le bois en particulier est un très bon matériau. On lui reproche surtout un manque de constance (la densité comme la résistance du balsa peut varier d’un facteur de 1 pour 3 dans un même lot,…). Le bois, s’il est utilisé dans des endroits stratégiques devra donc impérativement être pesé !

Le contreplaqué a des caractéristiques plus constantes grâce à la colle incorporée. Le hêtre pourra être remplacé par du bouleau à la fibre moins fine, mais moins cher.

Les métaux (fer, aluminium) ne doivent être utilisés que sous forme d’alliages (corde à piano, Dural). Leur principales qualités sont la malléabilité, la reproductivité des caractéristiques et l’isotropie.

Les composites époxy (verre, carbone, aramide), sont indiscutablement les matériaux rois, mais ils sont relativement coûteux et compliqués à mettre en œuvre. On observera en particulier que le composite carbone unidrectionnel (c'est-à-dire la tige ou le tube de carbone) est le matériau miracle pour alléger un modèle. De plus, sa raideur limite les déformations au mieux. L’aramide a surtout comme qualité le fait d’être ductile contrairement au carbone (il plie mais ne rompt pas, par contre il est très pénible à découper sans outillage spécial).

Concernant la contrainte maximale, il est important de savoir que du fait des incertitudes sur la valeur des efforts, des concentrations de contraintes et des hétérogénéité inévitables des matériaux, on utilise toujours en ingénierie un coefficient de sécurité entre la contrainte de rupture utilisée pour le calcul et celle affichée pour le matériau. Ce coefficient de sécurité est choisi entre 2 et 3 pour tous les cas courants. On peut prendre un coefficient inférieur à deux seulement si le matériau utilisé a été testé, si les efforts sont quasi-statiques et qu’il ne s’agit pas de pièces de sécurité. Lorsque le matériau est mal déterminé (bois) ou qu’il s’agit d’une pièce de sécurité on retient un coefficient de sécurité compris entre 3 et 5. Par exemple, pour une clef d’ailes en Dural, le matériau et les efforts sont bien déterminés, mais il s’agit d’une pièce de sécurité. On prendra donc autant que possible une coefficient de sécurité de 3, c'est-à-dire qu’on ne poussera pas le tube au-delà de 350/3 ≈120 N/mm².

Autres matériaux

L’ABS [4]

L’ABS est une matière plastique de qualité, très courante, qui est utilisée pour la fabrication en série de certains fuselages. Ca qualité principale est le faible coût de mise en œuvre en moulage sous vide. De nombreux fabricants proposent donc des modèles d’avions et planeurs économiques avec un fuselage en ABS. Comme l’ABS moulé sous vide donne des fuselages typiquement deux fois plus lourds que leur équivalant en composite, cette technique n’est pas utilisée pour les modèles de haut de gamme, ni pour la construction individuelle.

Le carton

Le carton est très rarement utilisé en modélisme. Comme c’est un dérivé du bois, il présente des caractéristiques mécaniques proches du bois ; il n’est donc pas à négliger. Sa densité est faible puisqu’il s’agit typiquement de deux feuilles de papier épais séparées par une troisième feuille ondulée. Bien utilisé, il peut parfaitement servir de base pour des avions qui seront construits et réparés à des coûts défiant toute concurrence. Une fois correctement peint ou verni, le carton est débarrassé de son principal défaut : sa sensibilité à l’humidité.

Il est même possible de réaliser des semi-maquettes comme l’a démontré François Paris sur la photo 2 ci-après :

Photo 2 : semi-maquette volante en papier et carton

La technique de construction est en cours d’élaboration, mais prouve d’ores et déjà la faisabilité. Il suffisait d’un aéromodéliste audacieux pour démontrer qu’on peut réaliser des aéromodèles avec des moyens limités !

Les matériaux expansés

Les matériaux expansés sont des matières plastiques remplies des myriades de micro-bulles de gaz. Il y a donc potentiellement autant de types de matières plastiques classiques que de matières plastiques expansées, la principale différence étant la présence des micro-bulles. La densité comme les caractéristiques mécaniques des matériaux expansés sont très variables, car tout dépend de la proportion de gaz dans le matériau ; typiquement plus de 99 % en volume. Les densités sont donc très faibles et varient typiquement de 0,015 à 0,04 (soit 15 kg/m³ à 40 kg/m³). Les caractéristiques dépendent au demeurant beaucoup plus de la densité choisie que de la matière plastique de base constituante.

Les matières plastiques [5] de base sont le polystyrène, le polyéthylène, le polypropylène et le polyuréthane. On utilise souvent un mélange et les fabricants donnent bien souvent des noms de marque à leur mélange. Le polystyrène expansé est le matériau le moins coûteux, mais présente une résistance à la traction médiocre. L’EPP (polypropylène expansé) est plus souple, possède une mémoire de forme et a une bien meilleure résistance à la traction, ce qui le rend très apprécié en modélisme. Par contre, comme il se moule difficilement, les grands fabricants ne l’apprécient pas trop. L’Elapor et l’Arcel sont composés de 70% polystyrène et 30% polyéthylène ; ils présentent un bon compromis entre qualités mécaniques et facilité de moulage d’où leur utilisation fréquente chez les fabricants qui sortent des modèles en grande série. Certains fabricants on d’ailleurs renoncé à utiliser toute autre technique de fabrication.

L’élaboration d’une pièce en expansé se fait typiquement en deux temps :

· le producteur de matière plastique élabore des petites billes de 1 à 2 mm de diamètre de matériau expansé,

· le transformateur (fabricant du modèle réduit) presse ensemble dans une atmosphère chaude (≈ 130°C) et humide les billes à l’intérieur d’un moule.

Le matériau étant constitué de billes collées entre elles par la chaleur, la résistance à la traction dépend beaucoup de la cohésion entre les billes, point faible du polystyrène expansé.

L’opération de moulage peut être pratiquée par des modélistes individuels car elle se fait à une température modérée permettant l’utilisation de moules en bois, mais ne présente réellement d’intérêt que pour une fabrication en série au sein d’un club.

Les matériaux extrudés

Les matériaux extrudés sont essentiellement de même nature que les matériaux expansés. La différence tient dans le mode d’élaboration. Au lieu d’utiliser des billes qu’on agglomère, on part directement d’un matériau pâteux qu’on fait passer sous pression à travers une filière [6]. Les formes utiles en modélisme sont essentiellement des feuilles de 3 ou 6 mm d’épaisseur. Les densités sont plus élevées que pour les matériaux expansés, variant typiquement de 25 à 50 kg/m³. Le Dépron et ses variantes, très utilisé dans notre hobby, est du polystyrène extrudé.

L’avantage de l’extrusion par rapport à l’expansion, en ce qui concerne le modélisme, est qu’il n’y a plus de billes qui adhèrent plus ou moins bien entre elles. La limite de traction s’en trouve donc fortement améliorée (τ max typique ≈ 30 N/mm²).

Avantage des matériaux à faible densité

A contrainte maximale admissible spécifique équivalente deux matériaux de densité différente donnent les mêmes résultats en traction puisqu’ils nécessitent la même masse de matière. Mais il n’en va pas de même en compression ou en flexion.

En effet, en compression, comme le matériau à faible densité aura une section plus forte, il résistera mieux au flambage. La différence est encore plus notable en flexion. En effet, dans le cas de la flexion d’une tige, la résistance (selon l’équation 7) vient autant de l’inertie quadratique (et donc du carré de la section de la tige) que de la contrainte maximale admissible ; or la très faible densité conduit à adopter une très forte section donc une inertie quadratique très élevée. De plus, la faible densité permet d’optimiser les formes et limiter la matière inutile.

Par exemple : une plaque d’extrudé de 3 mm et 90 g/m² résistera au flambage sur un fuselage ou un empennage. Une feuille de balsa plume de 1,5 mm et 120 g/m² ne fera pas mieux, et difficile de trouver plus léger ; tandis qu’un tissu de verre/époxy à 100 g/m², fin comme une feuille de papier n’aura strictement aucune capacité à résister au flambage.

N. B. : on peut considérer le bois comme un extrudé naturel, les bois les plus denses comme le gaïac (densité 1,4) ayant des contraintes maximales acceptables spécifiques très proches des moins denses comme le balsa. Toute la différence tient dans la proportion d’air par rapport à la matière organique.

Références

1. Loi de Hooke (Wikipédia)

2. Module de Young (Wikipédia)

3. Lois de Newton (Wikipédia)

4. ABS (Wikipédia)

5. Matériaux plastiques (Wikipédia)

6. Extrusion (Wikipédia)