Calculer son modèle réduit

Pour qu’un avion ou un aéromodèle puisse voler, à moins de profiter comme les planeurs des courants aériens, il lui faut un système de propulsion. Ce système peut se décomposer en quatre parties :

• L’hélice ou la turbine (qui est ni plus ni moins qu’une hélice carénée) qui est l’interface entre le moteur et l’air dans lequel le modèle vole. Elle fournit la force de traction Ft nécessaire au vol.

• Le moteur qui peut être électrique, à explosion (moteur à piston, maquette comme à la photo 1 ou non) ou une turbine à gaz. Il fournit la puissance Pt nécessaire à l’hélice afin qu’elle transforme puissance en force de traction Ft.

• Le contrôleur de puissance qui permet de régler la puissance fournie par le moteur. Il s’agit soit du servomoteur de gaz dans le cas des moteurs à explosion, soit du contrôleur électronique dans le cas des moteurs électriques.

• La source d’énergie. C’est le carburant dans le cas du moteur à explosion ou de la turbine à gaz. Ce sont les accumulateurs dans le cas des moteurs électriques. Comme dans ce cas il s’agit d’une source d’énergie secondaire (qui tire son énergie d’une autre source d’énergie), il faut aussi inclure le chargeur de batterie dans le système de propulsion, même si ce dernier n’est pas embarqué.

Dans ce chapitre nous allons étudier le premier de ces éléments : l’hélice, son principe et ses caractéristiques. L’adaptation de l’hélice au moteur à explosion et au moteur thermique seront traités au chapitres : « Propulsion par moteur thermique » et « La propulsion électrique ».

Le besoin de traction

La force de traction Ft (voir équation 1) sert à compenser les trois forces qui s’opposent à l’avancement de l’aéromodèle :

• la traînée aérodynamique Fx, égale à la composante perpendiculaire à la direction d’avancement du poids du modèle (masse m multipliée par la gravité terrestre g et le cosinus de l’angle de montée α) divisée par la finesse aérodynamique f du modèle dans la situation considérée.

• La force Fm qui s’oppose à la montée de l’aéromodèle. La force Fm est égale au poids m.g multiplié par le sinus de l’angle de montée α.

• La force Fa, conséquence de l’accélération de l’aéromodèle. La force Fa est égale à la masse m multipliée par l’accélération γ.

Traction = traînée + gravité + accélération (1)

On peut en déduire l’équation (2) détaillée ci-après :

Ft = Fx + Fm + Fa = m.g.cosα/f + m.g.sinα + m.γ (2)

Les équations 1 et 2 permettent de déduire qu’il faut fournir une force de traction pour compenser la traînée aérodynamique, mais aussi une force supplémentaire si on veut monter ou accélérer. Ces deux dernières forces ne doivent toutefois pas être considérées de la même façon que la traînée, car il s’agit d’un stockage d’énergie potentielle ou cinétique, énergie récupérée à chaque descente et chaque ralentissement. Ces composantes sont dites conservatives car elles peuvent être aussi bien positives que négatives, et sur un vol complet, la moyenne de Fm comme de Fa est nulle puisqu’on est en principe à la même vitesse (nulle) et altitude à la fin qu’au début de chaque vol.

Par exemple : notre « mini F3A » de référence de 2 kg (voir chapitre « domaine de vol ») lors d’une montée à 69 km/h avec une finesse f de 5,6 (voir feuille de calcul) selon une pente α de 60° accélérant légèrement de 1 m/s/s aura besoin d’une force de traction de :

Ft = 2x9,81x0,5/5,6 + 2x9,81x0,87 + 2x1 = 1,75 + 17 + 2 = 20,75 Newton, soit 2,1 kg

Cet exemple met en évidence comme ça a déjà été montré dans le chapitre « domaine de vol » que c’est avant tout pour monter qu’il faut tirer. C’est donc le taux de montée désiré qui va déterminer le dimensionnement du système de motorisation. Une maquette avec une pente de montée réaliste de 10 % se contentera d’une motorisation beaucoup plus modeste qu’un modèle de 3D qui doit pouvoir monter verticalement.

Accessoirement, la motorisation sert aussi à freiner dans les descentes. Toutefois, les hélices repliables sont incapables de remplir cette fonction et on aura la même situation avec les contrôleurs dont le frein électronique est débrayé. On sera alors parfois conduit dans ces deux cas, comme sur les planeurs et les avions à réaction, à utiliser des aérofreins.

Principe de l’hélice

L’hélice transmet la puissance du moteur à la masse d’air. Une vision simpliste, mais acceptable en première approximation, consiste à considérer que l’hélice se visse dans la masse d’air. Une analyse un peu plus fine montre que l’hélice, si elle se visse, accélère aussi la masse d’air environnante chassée vers l’arrière. La vitesse de l’air en aval de l’hélice est donc supérieure à la vitesse d’avancement de l’aéromodèle.

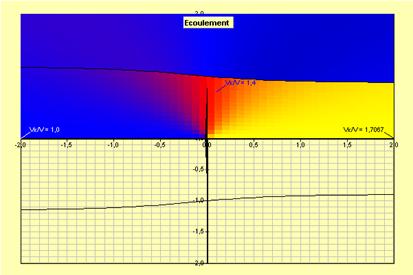
Froude a étudié ce phénomène pour les hélices de bateau et montré que la force de traction obtenue est proportionnelle à l’augmentation de vitesse ΔV de la masse de fluide, c'est-à-dire que sans augmentation de la vitesse du fluide (air ou eau) il n’y a pas de traction. La figure 1(obtenue avec Javaprop [1]) montre ce qui se passe. Sur cette figure, l’hélice est placée au centre et l’air est soufflé vers la droite de la figure. La couleur représente la vitesse de l’air en un point donné. La couleur bleue représente de l’air non accéléré, et plus on tend vers le jaune, plus l’air est accéléré. Loin en amont (extrème gauche), la vitesse de l’air par rapport au modèle est Vo (vitesse du modèle). Plus on s’approche de l’hélice, plus la masse d’air est accélérée ; l’augmentation de vitesse atteignant ΔV au niveau de l’hélice.

Au niveau de l’hélice, l’air concerné est bien sûr celui passant à travers le disque de l’hélice de section S = π.D²/4. Toutefois en amont, comme le montre la figure 1, la section concernée est plus élevée, car pour un débit donné constant, la section doit être d’autant plus importante que la vitesse est faible. En aval de l’hélice, l’air, paradoxalement, continue à s’accélérer jusqu’à une augmentation de vitesse finale de 2.ΔV, et la section d’air impliquée continue à diminuer avec l’augmentation de la vitesse de l’air.

Figure 1 : vitesse de l’air accéléré par une hélice

La force de traction Ft théorique ainsi fournie est donnée par l’équation de Froude (équation 3) en fonction de la densité ρ du fluide. C’est la formule de l’hélice parfaite qui a toujours un rendement de Froude η inférieur à 1, rendement donné par l’équation 4. Le rendement est inférieur à 1 car l’hélice fournit une puissance Pt = Ft.(V + ΔV) alors que le modèle ne récupère que la puissance utile Pt = Ft.V. Une hélice réelle qui a des pertes aérodynamiques pourra tendre vers ce rendement η sans jamais l’atteindre.

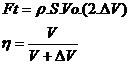(3)

(4)

Dans la pratique, avec les modèles réduits comme avec les avions de tourisme, l’accélération de la masse d’air reste très faible (de l’ordre de quelques pourcents) ; on dit alors que l’hélice est peu chargée. Dans le cas des turbines, la charge est beaucoup plus forte et il n’est pas exceptionnel dans ce cas de doubler la vitesse de la masse d’air, ce qui conduit inévitablement à des rendements de propulsion médiocres. Dans le cas des turbines à gaz où la vitesse d’éjection est le plus souvent supersonique (de l’ordre de Mach 1,4 à plein régime), s’ajoutent en plus les effets de la compressibilité de l’air.

Courbe de traction caractéristique, effet du pas

Figure 2 : courbes caractéristiques d’une hélice bipale 11"x5,5"

Figure 3 : courbes caractéristiques d’une hélice bipale 11"x7"

Figure 4 : courbes caractéristiques d’une hélice bipale 11"x10"

Les systèmes de propulsion à hélice ou turbine ont un rendement limité par quatre pertes de nature différente qui s’additionnent :

• la perte par accélération du flux d’air que l’on vient de voir déterminée par le rendement de Froude,

• la perte par friction de l’air sur la surface des pales, analogue à la traînée des ailes,

• la perte par tourbillon marginal correspondant strictement à la traînée induite d’une aile,

• la perte par déviation du flux d’air, résultant du fait qu’en arrière de l’hélice, l’air ne s’écoule pas en ligne droite, mais en spirale ; l’énergie supplémentaire non propulsive conférée ainsi à la masse d’air se traduisant par une perte supplémentaire.

En fin de compte, l’hélice se comporte un peu comme une aile avec une zone limitée de régime à bon rendement, et des rendements allant en diminuant lorsqu’on s’éloigne de cette zone optimale comme le montrent les figures 2, 3 et 4 obtenues avec logiciel libre de simulation d’hélices JAVAPROP [1] de Martin Hepperle.

N. B. : JAVAPROP peut être soit être utilisé sur le site sous forme d’applet (programme déporté sur un site Internet), soit en téléchargeant l’archive d’installation automatique javapropinstaller.msi de JAVAPROP tout en bas de la page de l’applet [2].

La figure 3 montre sous forme réduite ce qu’on peut attendre d’une hélice standard. L’expression « forme réduite » correspond au fait que plutôt que d’utiliser directement la vitesse V du modèle, la force de traction Ft générée par l’hélice et la puissance Pt fournie à l’hélice, on utilise leur variante sans dimension : respectivement l’avance Av, le coefficient de traction Ct et le coefficient de puissance Cp définis par les équations 5, 6 et 7 :

(5)

(6)

(7)

L’avantage de la forme réduite, c’est que pour des hélices de forme semblable on obtiendra des résultats indépendants du diamètre D en mètres, du régime de rotation N en tours/seconde, et de la masse volumique ρ de l’air en kg/m³.

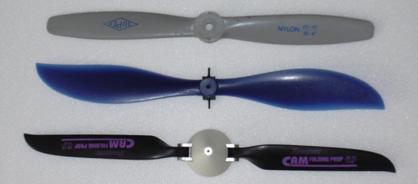
Par exemple : les courbes d’une hélice « nylon grise standard Graupner » (photo 2 haut) sont en principe valables pour toutes les hélices de la série pour peu que le pas relatif (Pas P divisé par le diamètre D) ne change pas trop, ce qui est bien commode pour faire son choix. L’élément qui influe le plus sur les courbes réduites est le pas relatif P/D, d’où les familles de courbes 2, 3 et 4 : la première étant représentative des hélices à faible pas relatif, la seconde représentative des hélices les plus courantes et la dernière représentative des hélices à fort pas relatif.

La courbe η^x en noir de la figure 3 indique le rendement de Froude de l’hélice (celui de l’hélice parfaite équivalente) qui tend vers 1 lorsque ΔV tend vers 0 (Av ≈ 0,7) alors que la courbe η en rose donne le rendement de l’hélice tenant compte de toutes les pertes. On remarque que lorsque ΔV tend vers 0, le rendement tend vers 0. Ceci est normal, car comme pour une aile, la traînée réduite Cx persiste alors que la portance réduite Cz s’annule lorsque la traction tend vers 0. Une hélice n’est donc pas efficace lorsqu’elle est utilisée pour une force de traction très inférieure à celle pour laquelle elle est conçue (par exemple hélice de modèle 3D utilisée pour faire du vol en palier).

La figure 3 montre aussi que lorsqu’on diminue la vitesse d’avance en dessous d’un seuil critique, le coefficient de traction stagne alors que le rendement diminue progressivement jusqu’à zéro pour une avance nulle. Ceci vient du fait que lorsque ΔV dépasse un seuil critique, les pales comme des ailes décrochent et le coefficient de portance Cz ne peut plus augmenter. Lorsqu’on mesure la force de traction d’une hélice à l’arrêt (sauf dans le cas d’un rotor d’hélicoptère) on mesure la force de traction maximale au décrochage. La force de traction à rendement maximal (donc celle obtenue normalement en vol) n’est en fait typiquement que de 40 % de cette valeur.

N.B. : les courbes Ct et Cp des figures 2, 3 et 4 proviennent d’une simulation dont le modèle, bien que très évolué, a des difficultés à prendre parfaitement en compte tous les effets du décrochage. En fait, dans les trois cas les courbes Ct et Cp sont plus régulières dans la réalité et tendent vers des horizontales lorsque Av est en dessous de 0,1 pour les figures 2 et 3 et en dessous de 0,2 pour la figure 4.

La figure 3 montre aussi que le rendement maximal d’une hélice est assez limité. Typiquement, il se situe entre 0,6 et 0,8.

Il est possible avec le logiciel JavaProp d’obtenir les caractéristiques complètes d’une hélice ou de trouver le dessin idéal d’une hélice si on souhaite en réaliser soi-même pour la compétition (racers). Les figures 1 à 5 ont au demeurant toutes été obtenues avec ce logiciel libre. La figure 5 donne le dessin d’une hélice bipale optimisée de 11"x7" (caractéristiques de la figure 3). On remarquera que la forme de la pale idéale n’est pas ellipsoïdale, contrairement à la forme de l’aile idéale. Ceci vient du fait que la vitesse augmente sur le profil au fur et à mesure que l’on s’approche de l’extrémité de la pale. La distribution de l’écoulement de l’air sur une pale est donc différente de celle sur une aile.

Figure 5 : cordes d’une hélice idéale

Le cas des pales d’hélicoptère est particulier. Le pas n’est pas constant le long des pales car c’est l’angle d’inclinaison β qui est constant tout au long des pales. De plus, le pas toujours très faible fait qu’on n’atteint jamais la zone de décrochage en vol normal. La courbe de traction obtenue avec des pales d’hélicoptère avec un calage normal s’approche de la courbe de la figure 2, mais avec une absence totale de zone de décrochage (zone irrégulière de gauche).

Choix du régime de rotation

L’équation 5 montre que la force de traction que peut fournir une hélice varie avec le carré de son régime de rotation. Il s’en suit qu’on a tendance à faire tourner très vite les hélices, d’autant plus que la puissance des moteurs thermiques et électriques est elle aussi proportionnelle au régime de rotation. Dans la pratique, l’extrémité des pales tournera souvent à la vitesse maximale de Mach 0,6 (0,6 fois la vitesse du son). C’est la limite si on ne veut pas subir les problèmes de compressibilité de l’air générant bruit et perte de rendement. Ceci conduit à une vitesse à l’extrémité des pales de 200 m/s soit environ 740 km/h.

Dans le cas des racers, on a besoin de pousser les hélices au maximum, ce qui conduit généralement à tourner plus vite : en général vers Mach 0,75. Ce n’est toutefois possible qu’en utilisant des profils supercritiques parfaitement adaptés (voir le chapitre sur l’aérodynamique et le site de Martin Hepperle [3] ) à faible Cz, sinon les ondes de choc supersoniques ruinent les performances.

Dans le cas des petits avions électriques lents (principalement slowfliers et indoor) on tourne moins vite. La vitesse d’extrémité de pales peut dans ce cas descendre jusqu’à 100 m/s (en deçà les hélices deviennent disproportionnées). Tourner relativement lentement est souvent une bonne idée, recommandée d’ailleurs par la FFAM, car le bruit des hélices augmente très rapidement avec la vitesse d’extrémité des pales.

Le tableau 1 donne le régime de rotation maximale en tr/mn pour des hélices de 6" à 15" pour une vitesse d’extrémité de pale de Mach 0,6 et 0,75. Mais il ne faut pas perdre de vue que certaines hélices devront être encore plus bridées pour des questions de résistance mécanique liées à la force centrifuge.

Diamètre	Régime à Mach 0,6	Régime à Mach 0,75
6"	25 000 tr/mn	31 000 tr/mn
8"	19 000 tr/mn	23 000 tr/mn
10"	15 000 tr/mn	19 000 tr/mn
12"	12 500 tr/mn	15 500 tr/mn
15"	10 000 tr/mn	12 500 tr/mn

Tableau 1 : régime de rotation des hélices en fonction de la vitesse de bout de pale

Choix du diamètre et du nombre de pales

Nous avons défini la force de traction Ft nécessaire dans le premier paragraphe de ce chapitre. L’équation 8 déduite de l’équation 6 nous permet de trouver le diamètre D adapté d’une l’hélice sous réserve de connaître Ct et N.

(8)

Pour trouver Ct il existe plusieurs méthodes :

• La première consiste à trouver Ct avec JAVAPROP, mais attention, le résultat risque d’être approximatif si on ne fait pas les bons choix ou si on fait des mesures approximatives (profils, angles d’inclinaison, …). Par contre, si on maîtrise bien l’outil, il donne des résultats étonnamment précis.

• La seconde consiste à mesurer la force de traction Ft à l’arrêt d’une l’hélice de la famille considérée et d’en déduire le Ct en statique de la famille grâce à l’équation 6.

• La dernière consiste à utiliser les règles empiriques ci-après provenant de l’expérience et de nombreuses mesures.

• Pour les hélices bipales standard grises Nylon Graupner, (photo 2 en haut) comme pour les hélices bipales APC, le Ct statique est d’environ 0,09 pour une hélice de 10"x7" (c’est la valeur la plus courante pour les hélices bipales de toutes sortes).

• Pour les petites hélices, on diminuera Ct (-0,01 pour une hélice de 6") ; a contrario pour une grosse hélice, on augmentera Ct (+0,02 pour une hélice de 15").

• Pour les hélices à faible pas relatif, on diminuera Ct (-0,01 pour P/D = 0,5) ; a contrario pour les hélices à grand pas relatif, on augmentera Ct (+0,01 pour P/D = 1).

• Pour les autres modèles d’hélices, on procédera par comparaison aux hélices Graupner ou APC en considérant que Ct est proportionnel à la surface relative des pales (l’hélice CAMPROP Graupner de la photo 2 en bas, par exemple, a le même Ct que l’hélice standard de la photo 2 en haut). L’influence du Czmax du profil est très importante aussi, mais en pratique les fabricants d’hélices utilisent tous des profils ayant des Czmax très proches, sauf dans le cas des hélices d’indoor qui sont très creuses et exceptionnellement porteuses (elles ont d’ailleurs aussi, bien souvent, des cordes relatives inhabituellement élevées comme le montre la photo 2 au centre).

Photo 2 : hélices de 10" à 11"

Un détail qui a son importance : comme la traction d’une hélice est proportionnelle à la surface des pales, elle est aussi proportionnelle au nombre de pales. Si une hélice bipale ne tire pas assez, une hélice de même diamètre et même corde moyenne à trois ou quatre pales fera peut être l’affaire ! Au demeurant, au début des années 30, les avions de chasse utilisaient des hélices bipales. Avec la montée en puissance des moteurs, les hélices avaient pratiquement toutes trois pales en 1939 sur les mêmes avions. Comme en 1945 la puissance avait encore augmenté, on était passé à quatre et parfois cinq pales sans changer significativement le diamètre et le régime de rotation …

Par exemple : notre « mini F3A » de référence a besoin d’une force de traction de 22,5 N (voir paragraphe : besoin de traction). Si on considère qu’on monte à la vitesse de 69 km/h alors que la vitesse en palier est de 106 km/h (c.f. feuille de calcul électronique) et que notre courbe de traction est celle de la figure 3, on peut en déduire par une règle de trois l’avance : Av = 0,7x69/106 = 0,46. Si on suppose que l’hélice est standard avec un Ct statique de 0,09, on peut en déduire notre Ct dynamique en le lisant directement sur la figure 3 : Ct = 0,044 pour Av = 0,46.

Si on sait à quel régime on tourne, on peut enfin calculer le diamètre de l’hélice en utilisant l’équation 8. Supposons par exemple qu’on tourne à 11000 tr/mn (183 t/s). Il vient alors :

La courbe puissance réduite Cp de la figure 3 nous donne une information supplémentaire. Le coefficient de puissance Cp est égal à 0,29 à notre point de fonctionnement Av = 0,46, mais on peut l’estimer à 0,35 pour une avance nulle, c'est-à-dire à l’arrêt au sol. Ceci signifie que la puissance absorbée par l’hélice à l’arrêt à 11000 tr/mn est 0,35/0,29 = 1,2 fois plus élevée à l’arrêt qu’en montée à 19 m/s. Si on utilise un moteur électrique, cela signifie que le courant au sol, image de la puissance, est 1,2 fois plus élevé que dans la montée. Donc si le moteur est dimensionné pour la montée il sera en surcharge à l’arrêt au sol. C’est tout à fait acceptable, à condition que ça ne dure pas, car les moteurs électriques acceptent très bien des surcharges durant 10 à 30 secondes mais pas plus.

Choix du pas

Le diamètre de l’hélice pour un régime donné définit la force de traction, à peu près constante à faible vitesse (ou avance), puis diminuant pour s’annuler à un certaine vitesse (ou avance) ; le diamètre de l’hélice est donc déterminé par la traction maximale désirée donnée par l’équation 2. Le pas, lui, définit la vitesse de vol à laquelle la traction chute puis s’annule ; le pas de l’hélice est donc fixé par la vitesse de vol maximale désirée en palier.

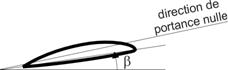
Figure 6 : pas d’une hélice

Par définition, le pas d’une hélice est la distance P qu’elle parcourt dans la masse de fluide (air ou eau) en un tour de rotation. Il y a toutefois une imprécision qui vient du fait qu’une hélice a un pas qui dépend des conditions de fonctionnement. A la limite, en stationnaire, toutes les hélices ont un pas effectif (celui observé par l’avancement du modèle) nul. On utilise donc un pas de référence qui n’est d’ailleurs pas unanimement reconnu. On pourrait prendre le pas pour lequel la traction de l’hélice est nulle. L’hélice se visserait alors dans l’air selon la direction de portance nulle représentée dans la figure 6. Malheureusement, ce pas bien pratique n’est pas donné pour les hélices. Le pas indiqué le plus généralement est le pas dit « géométrique ». Il correspond au pas de la corde de référence du profil, c'est-à-dire au pas donné par l’angle β de la figure 6 qui montre la coupe d’une pale d’une hélice de diamètre D au rayon r. Ce pas géométrique P est défini par l’équation 9 :

P = r.tanβ (9)

Pour ce pas, l’hélice fournit une force de traction modérée mais non négligeable. Le pas effectif Peff est le pas réel dans des conditions de vol données, pas en général inférieur au pas géométrique P. Le pas effectif Peff donné par l’équation 10 est plus petit que P d’une fraction nommée recul R (R compris entre 0 et 1).

Peff = (1 – R).P (10)

Le recul R à la vitesse maximale d’un modèle est une valeur importante car elle permet de choisir le pas géométrique P de l’hélice grâce à l’équation 11 dans laquelle N est le régime de rotation de l’hélice en tr/mn.

(11)

Le recul R est de l’ordre de 0,3 pour un modèle standard, il peut même être supérieur pour un modèle qui grimpe peu (maquette réaliste). Par contre, pour un avion d’acrobatie il est de l’ordre de 0,1 et peut même devenir nul pour un modèle de 3D.

Pour connaître le recul réel, il faut relever la force de traction Ft nécessaire au modèle à vitesse maximum, prendre les courbes de plusieurs hélices du bon diamètre mais de pas différents et trouver celle qui donne la traction la plus proche de Ft à la vitesse choisie.

Par exemple : notre « mini F3A » de référence a une vitesse maximale prévue d’environ 106 km/h (29 m/s) et une traînée en palier de 7,7 N à cette vitesse (voir feuille de calcul électronique). Si on suppose un recul de 0,1, l’équation 10 nous donne :

Si on observe la courbe de traction d’une l’hélice 13"x7" APC Standard générée par JavaProp à 11000 t/m, on observe une force de traction de 12 N à 29 m/s, supérieure aux 7,7 N de traînée. Ceci montre que notre hypothèse de recul de 0,1 est légèrement exagérée mais acceptable.

L’hélice de 13"x7" APC Standard convient donc a priori pour notre « mini F3A » s’il est équipé d’un moteur électrique tournant à 11000 tr/mn.

Malheureusement, les choses ne se passent pas toujours aussi bien, d’ailleurs dans le cas présent aucune hélice de série « électrique » n’a pu être trouvée, car tous les diamètres et tous les pas ne sont pas disponibles (qu’aurait t’on fait si on avait trouvé un pas de 6,5 ou pire de 12 alors qu’aucun pas de plus de 10 n’est proposé par les fabricants ?). De plus, comme tous les fabricants ne mesurent pas les pas de la même façon (c’est le même problème qu’avec les pointures de chaussures…) il convient en fait de prendre le pas le plus le proche trouvé par calcul puis faire des essais.

L’opération peut s’avérer laborieuse. Heureusement, il y a une solution peu connue en France, mais bien mieux en Allemagne toujours en avance dans le domaine du modélisme : l’hélice à pas réglable. Comme le nom le suggère, il s’agit d’hélices dont on peut régler le pas au sol à volonté. Seul le fabricant allemand RAMOSER [4] propose ce produit nommé VARIOPROP. Il est disponible sur Internet et en France dans quelques magasins. Ces hélices mériteraient d’être mieux connues (publicité gratuite) à plus d’un titre, car non seulement on peut régler leur pas, mais de plus elles existent en bipales, tripales et quadripales de plusieurs formes dont des formes maquette (voir photo 3). Une maquette sera incomparablement plus réaliste avec une tripale VARIOPROP bien choisie qu’avec une de nos sempiternelles bipales grises.

Photo 3 : pales "maquette" pour hélices à pas réglable VARIOPROP

Estimation du rendement

Connaître le rendement des hélices est important, car il influe sur le dimensionnement du moteur placé en amont. La valeur la plus juste du rendement est donnée par le logiciel JavaProp déjà mentionné dans ce chapitre (voir figures 2 à 4). Si on ne veut ou ne peut pas l’utiliser, on peut se contenter d’observer et retenir les résultats des figures 2, 3 et 4 qui sont typiques. Le rendement d’une bonne hélice tourne autour de 0,7 à son meilleur point de fonctionnement appelé point de conception. Il est intéressant toutefois de noter le résultat bien connu suivant :

• les hélices à faible pas relatif (P/D < 0,5) ont un rendement plus faible qui peut être aussi bas que 0,6 (figure 2),

• les hélices à fort pas relatif (P/D ≈ 1) ont le meilleur rendement qui peut atteindre 0,8 (figure 4).

Le dernier constat est d’ailleurs celui qui justifie qu’on utilise en F5B des hélices de grand diamètre tournant lentement. En effet, si on augmente de diamètre, pour maintenir Ft constant on va diminuer N, ce qui va conduire à augmenter le pas P encore plus que le diamètre D pour compenser. Ainsi, plus on diminue N, plus on augmente P/D pour maintenir constante la force de traction en vol en palier. Ceci permet en choisissant bien N d’atteindre l’idéal P=D ; valeur qui définit une hélice dite « carrée » (même si sa forme observable reste très différente !). L’inconvénient de ce procédé est que l’hélice plus grande est aussi plus lourde, et que la méthode ne peut s’appliquer que si on utilise un réducteur car sinon on est obligé de surdimensionner aussi le moteur dont l’embonpoint inutile devient alors trop pénalisant.

Références

1. Logiciel libre de simulation d’hélices de Martin Hepperle JAVAPROP

2. Page de téléchargement de l’archive de l’exécutable Java de JAVAPROP

3. Site de modélisme de Martin Hepperle

4. Fabricant allemand d’hélices à pas réglable RAMOSER