Aéromodélisme RC

Techniques et conception

La contrôlabilité et la stabilité

Lien vers « Sauver un animal »

Sommaire général

Auteur : Philippe Kauffmann

Version initiale : mars 2006

Dernière révision : 9 avril 2013

Photos : constructeur ou auteur, sauf mention contraire

N. B. : double-cliquer sur les images permet souvent d’obtenir une version agrandie.

Sommaire

Principe de contrôlabilité et stabilité

Le contrôle

Contrôle en roulis

Contrôle en lacet et tangage : l’empennage

Empennage en croix

Empennage en T

Empennage en V

Empennage canard

Dimensionnement d’un empennage

La stabilité d’un modèle

Notions de base sur la stabilité

Vibrations à haute fréquence (flutter)

Oscillations et amortissement

La stabilité en lacet

La stabilité en roulis

La stabilité en tangage

Equilibre statique

Calcul de stabilité dynamique simplifié

Réglage de la stabilité selon le type d’empennage

Les interactions entre les axes

Les modèles à empennage canard

Contrôle

Equilibre et stabilité dynamique

Les divers types d’ailes volantes

Utilisation d’un profil autostable

Utilisation d’ailes en flèche vrillées

Les biplans et multi-plans

Les biplans classiques

Observation

Analyse

Optimisation

Deux plans en tandem

Observation

Analyse

Optimisation

Plus de deux plans

Les configurations inhabituelles

Premier « Avion »

Stabilisateur devant et derrière

Le cas de l’hélicoptère

Principe de base de l’hélicoptère

Les deux formules principales

Solution avec rotor anti-couple

Formule birotor

Le pilotage

Les quatre axes de commande

Le problème de la stabilité

Stabilité en montée et descente

Stabilité en lacet

Stabilité en roulis et tangage

Les réglages

Calage des pales

Réglage du gyroscope

Choix des débattements

Réglage de la stabilité en roulis et tangage

Références

Principe de contrôlabilité et stabilité

Il est évident que pour qu’un aéromodèle présente un intérêt, il doit être pilotable et donc contrôlable. Ca n’a pas toujours été aussi évident car l’ « Avion » de Clément Ader [1] n’avait a priori pas d’organes de contrôle efficaces… Pire, la stabilité, c'est-à-dire la capacité à rester dans une direction donnée n’avait pas été étudiée.

N. B. : l’impossibilité de voler des avions d’Ader a largement été démontrée par Alain Vassel par une étude de plusieurs années ayant conduit à la réalisation de plusieurs maquettes. L’étude est diffusée dans un document très complet diffusé sur Internet [2].

Le modélisme, lui, est apparu et c’est développé à partir des modèles de « vol libre » sans organe de contrôle. A cette époque on a recherché les critères permettant de garantir et maximiser la capacité des modèles à se maintenir en ligne droite (ce qui n’est pas naturel du tout pour un aéromodèle), donc la stabilité. On s’est alors immédiatement aperçu que la stabilité ne devait pas se limiter à la capacité à maintenir une direction de vol, mais devait englober la capacité à revenir en ligne droite après une perturbation externe induite (turbulence atmosphérique ou rafale de vent).

Avec l’avènement de la radiocommande il a fallu ajouter la contrôlabilité à la stabilité comme pour les avions « grandeur » en ajoutant les mêmes organes de contrôle. L’aéromodélisme a profité de l’expérience acquise avec les premiers avions et n’a pas utilisé le vrillage des ailes ni l’empennage canard des premiers avions des frères Wright [3]. Comme la contrôlabilité s’oppose d’une certaine façon à la stabilité, on a alors diminué la stabilité en ne préservant qu’une légère propension à « revenir » après une perturbation. Cette propension à revenir, qualifiée de « degré de stabilité » est d’ailleurs choisie bien plus forte pour un modèle de début que pour un modèle d’acrobatie. Au demeurant, un modèle parfaitement neutre, c'est-à-dire à la limite entre la stabilité et la l’instabilité (propension à changer spontanément d’attitude) est parfaitement pilotable par un modéliste quelque peu entrainé.

L’aéromodèle évoluant dans un univers à trois dimensions la contrôlabilité et la stabilité sont étudiées traditionnellement indépendamment en roulis (rotation autour de l’axe d’avancement), tangage (basculement d’avant en arrière en vol horizontal) et lacet (rotation autour d’un axe vertical en vol horizontal). Ceci n’empêche pas qu’un mouvement autour d’un des ses trois axes de rotation perpendiculaires puisse induire un mouvement autour d’un des deux autres axes ; phénomène baptisé « interaction entre les axes ».

Le contrôle

Le contrôle s’obtient le plus souvent en articulant à l’aide d’un servomoteur une partie mobile à l’arrière des surfaces aérodynamiques (ailes ou empennages) couvrant typiquement 25 % de la corde. Il est aussi possible d’articuler l’ensemble d’une surface aérodynamique, ce qui rend le contrôle très efficace, mais reste délicat à réaliser car un jeu mécanique excessif ou un mauvais placement du centre de rotation risque d’engendrer du « flutter » (vibration dangereuse). Dans certains cas très rares (maquette ancienne) on utilise le contrôle du vrillage des surfaces des ailes à la place de surfaces mobiles pour rester conforme à la technique utilisée sur l’original.

L’efficacité du contrôle dépend de trois critères principaux :

· la vitesse du modèle,

· le débattement de la gouverne,

· et la portion de corde utilisée par la gouverne.

Comme la sensibilité des gouvernes augmente fortement avec la vitesse, les avions rapides peuvent se contenter de gouvernes réduites, tandis que les modèles « indoor » très lents exigent des gouvernes surdimensionnées. Les modèles à forte plage de vitesse, quant à eux, imposent souvent l’utilisation du « dual rate » (double débattement) ; débattement fort à faible vitesse et débattement réduit à forte vitesse. De nombreux modélistes utilisent l’exponentiel (diminution de la sensibilité à proximité immédiate du neutre) en lieu et place du double débattement. Ce n’est pas équivalent au double débattement car si à grande vitesse on obtient un contrôle satisfaisant, a contrario, à petite vitesse lorsqu’on utilise la totalité de la course des servos, la précision de pilotage est diminuée en raison de la sensibilité accrue dans le domaine des grands débattements.

Le réglage du débattement semble à première vue être le moyen idéal de régler la sensibilité des gouvernes. Ce n’est en fait pas aussi simple car on obtient une réponse linéaire des gouvernes par rapport aux servos seulement si le débattement angulaire de la gouverne est le même que celui du servo de commande (longueur du palonnier identique à celui de la chape correspondante). De plus, si on limite à l’émetteur la course du servo, la précision s’en trouve affectée.

Du constat précédant il résulte que dans la mesure du possible on se place dans le cas d’une commande directe (longueur palonnier servo = longueur chape) et on adapte la dimension et donc la corde et la longueur de chaque gouverne en fonction de la sensibilité désirée. Malheureusement, ce n’est pas toujours possible ; en particulier pour les modèles 3D où on est souvent obligé d’augmenter le débattement des gouvernes.

Contrôle en roulis

Le contrôle en roulis s’obtient classiquement par des ailerons qui s’étalent typiquement sur les 40 % externes des ailes comme sur les avions grandeur. Mais une autre disposition, spécifique au modélisme est aussi souvent utilisée : les ailerons « full span » (pleine envergure) qui s’étalent sur toute l’envergure des ailes. Comme elles occupent tout le bord de fuite de l’emplanture au saumon, on réduit en général leur corde à 15 % de la corde moyenne des ailes. Cette disposition présente deux avantages :

· commande facile des deux ailerons à partir d’un servo unique placé entre les deux ailes,

· une partie des ailerons est soufflée par l’hélice, ce qui permet de conserver de l’efficacité à vitesse nulle.

Les modèles indoor (vol lent) et 3D (qui peuvent faire du sur place) ont impérativement besoin d’ailerons « full span » car ils ne peuvent pas se passer de l’effet du souffle de l’hélice.

.

Contrôle en lacet et tangage : l’empennage

L’empennage traditionnellement placé à l’extrémité arrière de l’avion permet le contrôle en tangage et lacet. On distingue plusieurs types d’empennage :

Empennage en croix

C’est l’empennage le plus classique. Il est constitué de deux parties :

· D’une partie verticale appelée en général « dérive » par analogie avec la surface verticale des bateaux à voile. Dans le cas d’un avion, la dérive sert à contrôler le mouvement en lacet. En pilotage traditionnel, cette surface est peu utilisée et sert uniquement à garantir la symétrie de vol (éviter l’avancement en « crabe »). Les modèles simplifiés se passent souvent de commande sur cet axe car on se préoccupe peu dans ce cas de la symétrie du vol.

· D’une partie horizontale, ensemble de deux ailes miniaturisées. Cette partie sert au contrôle en tangage, et c’est donc cette surface aérodynamique qui permet de faire monter ou descendre l’aéromodèle.

Empennage en T

Dans cette variante, la partie horizontale de l’empennage est placée au dessus de la dérive. Cette disposition rend l’empennage beaucoup plus efficace car il n’est plus dans les turbulences des ailes, De plus l’empennage horizontal est alors protégé du sol en cas d’atterrissage sur terrain inégal, élément important pour un planeur qui ne dispose pas de train d’atterrissage.

Empennage en V

L’empennage en V est composé de deux surfaces inclinées placées symétriquement formant entre elles un angle de 110 ° (parfois 120°). L’avantage de cette formule est qu’on supprime une surface aérodynamique et qu’on diminue donc un peu la trainée, ce qui peut être important en planeur de compétition. La contrepartie est que la commande des gouvernes doit se faire par deux servos (un par gouverne) avec un mixage électronique à l’émetteur entre les deux servos.

Empennage canard

Lorsque l’empennage horizontal est placé à l’avant plutôt qu’à l’arrière on parle d’empennage canard. C’est une disposition rarement utilisée car elle est délicate à mettre au point. En effet l’empennage est alors déstabilisant et compense une stabilité excessive des ailes. Pour éviter les vrilles à plat, l’empennage canard doit impérativement décrocher avant les ailes, ce qui impose un dimensionnement très précis (voir à la fin de ce chapitre).

Dimensionnement d’un empennage

Les avions des pionniers utilisaient des empennages très petits, suffisants pour contrôler les avions aux vitesses et attitudes normales, mais parfois insuffisants dans les cas extrêmes. De plus, ces empennages ne conféraient pas une bonne stabilité, ce qui pose problème lorsqu’on veut réaliser une maquette sans tricher sur les proportions. Aujourd’hui, les avions grandeurs, comme les modèles réduits utilisent des empennages largement dimensionnés.

Les dimensions typiques sont :

Bras de levier (distance entre foyer des ailes et foyer de l’empennage) : autour de trois fois la corde moyenne des ailes

Surface de dérive : environ un douzième de la surface des ailes

Surface de l’empennage horizontal : environ un quart de la surface des ailes

Lorsqu’on augmente le bras de levier on peut diminuer les surfaces. Un bras de levier et des surfaces plus grands améliorent l’amortissement de l’aéromodèle (voir les détails dans la suite chapitre).

La stabilité d’un modèle

Notions de base sur la stabilité

Comme expliqué brièvement au début du chapitre, un aéromodèle doit avoir une tendance naturelle à évoluer en ligne droite, y compris après une perturbation externe induite (turbulence atmosphérique ou rafale de vent) ; c’est la stabilité. En cas de perturbation ou ordre bref sur une gouverne, un modèle stable dévie d’abord plus ou moins vite en fonction de l’importance de l’action et de l’inertie du modèle, puis va se stabiliser dans une nouvelle direction après avoir oscillé plus ou moins longtemps autour de la nouvelle direction (cf. figure 2). On notera à ce propos deux points :

· L’effet d’un ordre sur une gouverne n’est jamais instantané, mais toujours limité par l’inertie ; inertie d’autant plus élevée que le modèle est gros. Sur les bombardiers de la seconde guerre mondiale de type B17 il fallait attendre plusieurs secondes entre un ordre donné aux ailerons et un effet significatif sur l’inclinaison.

· La stabilisation n’est jamais parfaite, mais toujours traduite par un temps plus ou moins important pour atteindre la nouvelle position stable, soit par une oscillation plus ou moins rapidement amortie autour de la future nouvelle position stable.

Il va de soi qu’un aéromodèle mal étudié peut être instable. Dans ce cas, il refuse de rester dans une direction donnée sans corrections continuelles ; c’est comme un crayon debout sur la pointe qui ne reste debout que si on le tient dans le creux de sa main et en la déplaçant pour compenser la tendance spontanée à tomber. Ceci étant précisé, un avion instable n’est pas nécessairement un mauvais avion puisque les avions de combats modernes sont presque tous instables et contrôlés par des stabilisateurs électroniques. Ce type de système de stabilisation est déjà utilisé par certains pilotes de maquettes d’hélicoptère (dispositifs « flybar less »).

Les vibrations à haute fréquence (flutter)

En plus des problèmes d’oscillation normale autour de chaque axe (roulis, tangage et lacet), les gouvernes peuvent présenter dans certaines conditions (haute vitesse) des oscillations très rapides (vibrations) appelées « flutter » qui se propagent par aéroélasticité à toute la cellule. Cela peut finir par une perte de contrôle et une désagrégation du modèle. Le problème est engendré par une instabilité aérodynamique de la partie mobile de la gouverne et est accentué par les jeux et l’élasticité dans la commande. Ce phénomène est sans rapport avec les oscillations à faible fréquence (quelques Hertz) liées à la stabilité qui provoque un mouvement global, mais pas une déformation du modèle.

Oscillations et amortissement

Pour bien comprendre les comportements (mouvements) liés à la stabilité, on se propose d’étudier ici de façon précise l’expérience simple de la girouette.

Supposons qu’une aile de masse négligeable de surface S et de pente de portance a est fixée au bout d’une tige de longueur L (distance entre l’axe de rotation et le foyer de l’aile) ayant une inertie représentée par deux petites masses m/2 à distance l de l’axe de rotation (figure 1).

Figure 1 : action sur une girouette dans le vent

Si on met cette girouette dans un flux d’air de masse volumique ρ à vitesse Vt et qu’on la dévie brusquement d’un angle α de sa position de repos, elle reviendra à sa position initiale selon une des trois courbes de la figure 2.

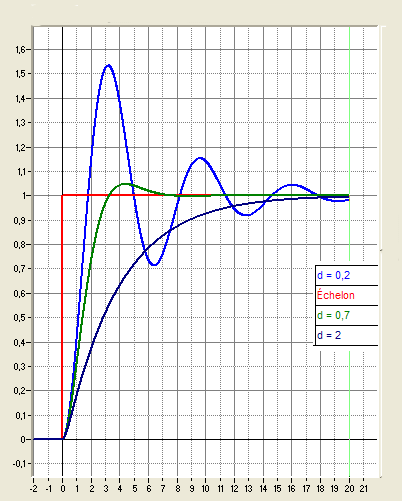
Figure 2 : courbes de retour à l’équilibre d’une girouette après une perturbation en fonction du coefficient d’amortissement

On observe en général une oscillation de période P appelée période propre et d’amortissement d plus ou moins élevé. L’amortissement défini par l’équation 2 traduit la rapidité d’atténuation de l’oscillation.

La résolution mathématique du problème donne la valeur P (équation 1) pour la période propre et la valeur d (équation 2) pour le degré d’amortissement. Il n’y a effectivement oscillation que si le facteur d’amortissement d est inférieur à 1 (courbe d = 0,2 de la figure 2). Dans le cas contraire, il y a un retour plus ou moins lent au neutre selon la valeur de d (courbe d = 2 figure 2). On admet en général que le meilleur comportement est obtenu pour le cas limite d = 0,7 (courbe d = 0,7 figure 2) qui présente un léger dépassement, mais pas d’oscillation significative. De façon générale, trop amortir est gênant car le temps retour au repos s’allonge et ne pas amortir assez provoque des oscillations d’amplitude gênante et qui durent trop longtemps.

On remarquera que le phénomène évoqué ici est très général. C’est le problème qu’on retrouve aussi dans tous les systèmes à ressort comme les suspensions de voiture par exemple. Pour qu’une suspension de voiture fonctionne correctement il faut amortir la tendance naturelle du ressort de suspension à osciller à l’aide d’un amortisseur qui doit être remplacé lorsqu’il est usé. Avec un amortisseur usé, la suspension se met à osciller à chaque passage dans un trou ou dénivelé subit.

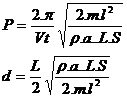
(1)

(2)

Dans les équations 1 et 2, le produit m.l² représente le moment d’inertie I du système selon l’axe considéré, tandis que le terme r.a.L.S/2 représente l’efficacité de la surface aérodynamique. On peut donc en déduite que la fréquence d’oscillation (inverse de P qui est la période de l’oscillation) est proportionnelle à la vitesse de l’air Vt, augmente avec l’efficacité de la surface aérodynamique et diminue avec le moment d’inertie. De la même façon on peut constater que l’amortissement d est proportionnel au bras de levier L (facteur prépondérant) mais qu’il est aussi amélioré par l’efficacité de la surface aérodynamique et détérioré par le moment d’inertie.

La stabilité en lacet

On peut facilement assimiler la girouette à l’axe de lacet d’un aéronef. Dans ce cas, la surface aérodynamique est celle de la dérive, le moment d’inertie est celui de la cellule selon l’axe de lacet et le bras de levier est la distance entre le foyer de la dérive et le centre de masse de l’aéronef ; l’oscillation se faisant autour du centre de masse.

Si on donne une impulsion sur la commande de dérive, après l’écart initial et si d est inférieur à 0,7 on pourra observer l’oscillation. Elle est en général parfaitement observable car nos modèles ne sont bien souvent trop amortis selon cet axe. Dans ce cas, en augmentant d (c'est-à-dire le bras de levier L ou la surface de la dérive) on obtiendra des trajectoires plus nettes.

Tout le monde a observé que les modèles de F3A ont un fuselage très long, aussi long que le permet par le règlement. C’est naturellement pour augmenter l’amortissement et donc permettre des trajectoires plus « nettes ».

On notera que le moment d’inertie I est matérialisé par le produit m.l², ce qui signifie que même si on ne peut pas jouer sur la masse, il est possible de diminuer le moment d’inertie en concentrant tous les éléments (radio, batteries, servos,…) au voisinage immédiat du centre de masse. En fait, comme il faut respecter le centrage (explicité plus loin) on n’obtient le meilleur résultat qu’en jouant sur l’élément critique qui est la queue. Plus on allègera la queue, plus on pourra reculer le moteur et plus l’aéronef sera agile. Les chasseurs de la première guerre mondiale étaient très agiles car leur queue était très légère, ce qui permettait de fortement rapprocher le moteur du centre de masse (photo 1).

Photo 1 : Sopwith Camel. Noter la proximité des éléments lourds (moteur, train) avec le centre de masse (photo wikipédia)

Ceci étant, ce n’est pas forcément toujours une bonne idée de chercher à diminuer le moment d’inertie. En effet, un modèle se comporte comme un modèle plus gros si on augmente son moment d’inertie, il se déstabilise moins vite et est par conséquent plus facile à contrôler ; ce qui n’est pas à négliger pour un débutant ou pour l’entraînement au torque roll et autres figures un peu difficiles.

Le simulateur Aérocalc analyse ce problème oscillatoire dans le panneau « Construction – stabilité – autonomie » en tenant compte de l’influence du fuselage pour un résultat plus précis. Pour le petit avion d’acrobatie EXTANA de Telink, la période d’oscillation en lacet calculée par Aérocalc est 0,43 s et l’amortissement 0,21 à une vitesse de trois fois la vitesse de décrochage, ce qui conduit à l’oscillation amortie visible à la figure 3. La médiocrité de l’amortissement s’explique ici par le fait que la queue de cet avion est relativement courte, à l’image de l’EXTRA 300 qu’il copie librement.

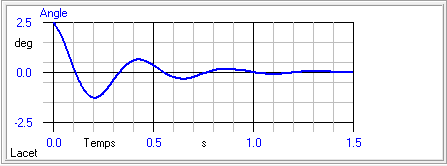
Figure 3 : oscillation amortie en lacet de l’EXTANA (copie d’écran d’Aérocalc)

La stabilité en roulis

Concernant l’axe de roulis, l’assimilation à l’expérience de la girouette n’est pas possible. Deux options sont possibles :

· Peu ou pas de stabilité. Comme la période d’oscillation et l’amortissement sont très élevés selon cet axe en raison de la surface des ailes qui est très grande comparée à l’empennage, la stabilité n’est pas une nécessité. Un comportement neutre ou une stabilité légèrement négative est parfaitement acceptable. On utilise alors des ailes médianes ou basses.

· Stabilité positive. Les débutants ont besoin de stabilité en roulis pour faciliter l’apprentissage. Dans ce cas on fait en sorte que le centre de masse soit sous le centre de portance des ailes. Plus la distance verticale entre les deux points est importante, meilleure est la stabilité en roulis. Pour que cette distance soit positive on utilise des ailes hautes ; pour l’augmenter on augmente la hauteur de la « cabane » (partie qui porte les ailes et qui représente l’habitacle de l’avion). L’ajout d’un dièdre sur les ailes augmente encore cette distance et donc la stabilité en roulis.

Le système d’équations permettant de calculer les paramètres est différent de celui de l’axe de lacet, car on est ici en présence d’un pendule amorti avec un amortissement qui n’est plus indépendant de la vitesse. Pour l’EXTANA de Telink la période d’oscillation calculée par Aérocalc est 9,94 s et l’amortissement 6,84 à trois fois la vitesse de décrochage, ce qui conduit à la courbe presque plate visible à la figure 4. On peut constater ici qu’étant donné le fort coefficient d’amortissement, le modèle tend à conserver son inclinaison après la perturbation. La période d’oscillation est dans le cas présent très élevée car elle varie à l’inverse de la distance entre le centre de masse et le centre de poussée des ailes qui n’est que de 1,1 cm dans le cas de l’EXTANA.

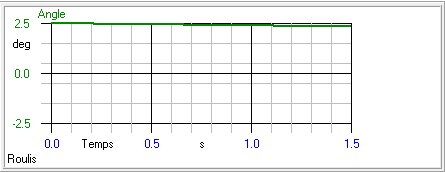
Figure 4 : effet d’une perturbation en roulis de l’EXTANA (copie d’écran d’Aérocalc)

La stabilité en tangage

L’étude de la stabilité en tangage est encore plus compliquée qu’en roulis car on cumule l’effet « Girouette » et l’effet « Pendule ». De plus, Il faudra d’abord faire en sorte que l’aéronef soit équilibré vis-à-vis de la gravité (équilibre statique) et seulement dans un deuxième temps prendre en compte la stabilité dynamique. Si le centre de poussée des ailes se situe au-dessus du centre de masse ─cas de tous les modèles à ailes hautes─ on profitera de « l’effet pendule » qui raccourcit la période d’oscillation tout en augmentant l’amortissement. Par contre dans le cas contraire, le système pourra devenir instable dynamiquement, (divergence au lieu d’oscillation) même s’il est équilibré statiquement. Aérocalc permet de mettre ce problème en évidence grâce à une mise en équations précise du modèle étudié.

Dans le cas l’EXTANA de Telink la période d’oscillation en tangage calculée à trois fois la vitesse de décrochage par Aérocalc est 0,28 s et l’amortissement 0,32, ce qui conduit à la courbe d’oscillations amorties de la figure 5. La période d’oscillation est plus courte qu’en lacet du fait du moment d’inertie plus faible du modèle selon cet axe (moindre influence des ailes) et l’amortissement est un peu meilleur du fait de l’effet de la gravité, bien que le centre de masse soit très près du centre de poussée des ailes dans ce cas précis.

Figure 5 : oscillation amortie en tangage de l’EXTANA (copie d’écran d’Aérocalc)

Equilibre statique

L’équilibre statique présenté à la figure 6 est obtenu lorsque la somme des forces appliquées sur le modèle s’annulent, c'est-à-dire :

Fza = m.g + Fzs (3)

· Fza étant la portance des ailes,

· m.g le poids de l’aéromodèle, et

· Fzs étant la poussée vers le bas de l’empennage horizontal ;

ainsi le modèle ne monte ni ne descend, et lorsque que les moments s’annulent aussi (expression 4) :

Mo = ka.c.Fza + L. Fzs (4)

· Mo étant le moment piqueur des ailes (constante du profil à vitesse constante),

· ka.c étant la distance entre le centre de masse et le foyer (point neutre) des ailes (ka est l’expression en fraction de corde moyenne c de cette distance, souvent exprimée en pourcentage dans la pratique),

· ka.c.Fza étant le moment cabreur lié au décalage arrière du centre de masse par rapport au foyer (point neutre) des ailes, et

· L.Fzs étant le moment de rétablissement créé par l’empennage horizontal (L est la distance entre le centre de masse et le foyer de l’empennage) ;

Ainsi le modèle ne bascule ni vers l’avant ni vers l’arrière.

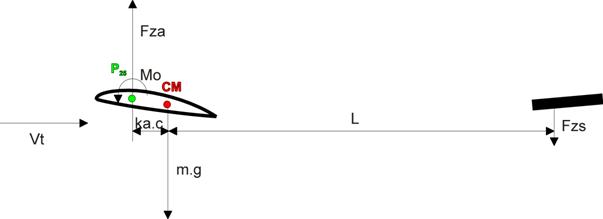
Figure 6 : forces et moments longitudinaux aérodynamiques appliqués sur un aéromodèle

La différence de calage angulaire entre les ailes et l’empennage horizontal s’appelle le V longitudinal. Cet angle doit être défini avec précision pour annuler les moments. Comme sa valeur dépend de la vitesse de vol, il faut l’ajuster en fonction de cette vitesse en agissant sur le trim de profondeur. Souvent trois points de réglage suffisent :

· Un réglage de trim pour le décollage et l’atterrissage,

· un autre pour le vol à vitesse de croisière,

· un dernier pour la vitesse maximale.

Lorsque le réglage est imparfait une action permanente sur la profondeur est nécessaire pour assurer une évolution en ligne droite ; sinon l’aéromodèle monte ou descend.

Précaution indispensable : il faut qu’aux fortes incidences (faibles vitesses) le stabilisateur décroche après les ailes sinon on entre dans le décrochage ou la vrille à plat dont on ne sort pas. De nombreuses personnes sont mortes avant que ce problème soit parfaitement compris. La solution consiste évidemment à mettre un stabilisateur de taille suffisante. Heureusement, les stabilisateurs sont aujourd’hui de taille beaucoup plus généreuse qu’au début du 20^ème siècle afin de favoriser l’amortissement, ce qui règle la question. Par contre, si on réalise des maquettes d’avions du début du 20^ème siècle il faudra prendre des précautions car leurs empennages sont souvent très petits et peu efficaces, ce qui peut rendre la maquette susceptible de rentrer dans une vrille à plat.

Calcul de stabilité dynamique simplifiée

La figure 7 permet d’étudier et expliquer la stabilité dynamique de façon simplifiée si on ne tient pas compte de la hauteur de la poussée des ailes par rapport au centre de masse et si on ne s’intéresse pas aux valeurs des périodes d’oscillation et amortissement. C’est la méthode universellement utilisée depuis toujours dans le cadre du modélisme ; c’était la seule envisageable tant qu’on n’avait pas d’ordinateur ni d’ingénieur à disposition.

Un aéronef est dit stable si lorsqu’on bascule le modèle légèrement en avant ou en arrière d’un angle dα à partir de la position de repos il a tendance à revenir naturellement à sa position initiale, exactement comme la girouette dans un flux d’air du paragraphe précédant. Pour cela, il faut que le moment déstabilisant ka.c.dFza induit par les ailes soit inférieur au moment stabilisant (qui tend à faire revenir à l’équilibre) L.dFzs du stabilisateur bien nommé. On notera que le préfixe d devant l’angle et les forces indique une petite variation d’angle et de force. En effet, on étudie ici uniquement des variations de moment, pas des moments. On remarquera également que dMo n’apparaît pas car le moment par rapport au foyer Mo est constant à vitesse constante, ce qui implique dMo = 0. Il en est de même pour le poids m.g qui ne varie pas non plus.

Figure 7 : moments de rappel aérodynamiques appliqués sur un modèle perturbé longitudinalement

Il faut donc que ka.c.dFza soit inférieur à L.dFzs. Or, on peut exprimer dFza et dFzs en fonction des lois de la portance des surfaces aérodynamiques en fonction de la vitesse d’avancement Vt. On en déduit les égalités 5 et 6 dans lesquelles r est la densité de l’air, ka est la distance P25-CM (soit le recul du centre de masse par rapport au foyer des ailes, exprimée en fraction de la corde moyenne c des ailes), aa et as sont respectivement les pentes de portance des ailes et de l’empennage, da est la variation d’incidence déstabilisatrice (voir figure 7) et Sa et Ss sont respectivement les surfaces utiles des ailes et de l’empennage. Le coefficient kα est un coefficient correcteur de dα pour tenir compte du fait que l’incidence varie moins vite sur le stabilisateur que sur les ailes, car les ailes dévient le flux d’air ; kα varie environ de 0,3 à 0,5 selon la longueur du fuselage. Le coefficient ks est un coefficient correcteur de Ss pour tenir compte du fait que le stabilisateur perd une partie de son efficacité lorsqu’il est dans les turbulences du fuselage ; ks qui est toujours inférieur à 1 dépend de la position du stabilisateur (voir au paragraphe sur les types d’empennage).

(5)

(6)

On tire donc des équations 5 et 6 la valeur maximale de ka acceptable :

(7)

Les quatre termes de droite de l’équation 7 : Sa (surface des ailes), Ss (surface du stabilisateur), L (bras de levier de l’empennage) et c (corde moyenne des ailes) forment une fraction parfois appelée « volume de stabilisateur », ce qui est spécieux puisque il s’agit d’un nombre sans dimension qui n’a de rapport avec aucun volume !

La valeur ka – si on admet l’égalité à l’équation 5 – donne une marge de stabilité nulle, i.e. un comportement neutre sur l’axe longitudinal. Pour un bon comportement il vaut mieux une marge de stabilité positive car la période propre est faible en modélisme. La marge de stabilité définit en fin de compte pour chaque modèle une période propre et un degré d’amortissement. En modélisme on prend en général une marge initiale de 5 % à 10 % de la corde moyenne des ailes, puis on déplace le centre de masse en avant et en arrière jusqu’à obtenir le comportement le plus satisfaisant.

Le calcul mathématique de la période propre et de l’amortissement selon l’axe longitudinal sortent du cadre de ce document de vulgarisation, car si le fuselage intervient peu, les ailes modifient considérablement l’amortissement. L’influence des ailes dépend de son coté beaucoup de la flèche éventuelle et de leur hauteur au-dessus du centre de masse. Aérocalc est parfaitement adapté pour conduire ce calcul avec le minimum d’effort car il détermine automatiquement les moments d’inertie, moments quadratiques, surfaces, centre de masse et autres données nécessaires en fonction des grandeurs géométriques et de masses fournies.

N. B. : L’équation 7 a été ici redémontrée car il circule des variantes plus ou moins fausses de cette équation dans le monde modéliste. Certaines des ces variantes proposent les marges de stabilité à retenir en fonction d’éléments qui en réalité n’influent pas sur la stabilité comme le galbe des ailes (il n’agit que sur l’équilibre car au foyer le moment de basculement est fixe) et ignorent des éléments essentiels comme l’inertie et la flèche des ailes dont l’influence sur l’amortissement est majeure. Certains logiciels payants donnent le point neutre, mais pour des raisons incompréhensibles font varier L qui est essentiellement une constante comme on vient de le voir puisque la position du foyer est fixe. On ne peut donc pas ce fier à ces outils.

Cas des ailes hautes

Dans le cas des modèles à ailes hautes, la figure 7 n’est plus exacte, car le point d’application de la portance se situe au-dessus du centre de masse, ce qui augmente la stabilité en vol normal. La disposition « ailes hautes » est donc toujours utilisée pour les avions de début puisque cette disposition améliore la stabilité aussi bien en tangage qu’en roulis. Malheureusement, si cela est vrai en vol normal, en vol inversé (vol dos) la stabilité est diminuée et le modèle peut même être instable. Les modèles à ailes hautes sont donc inadaptés à l’acrobatie, hormis quelques figures de base comme les boucles et les tonneaux.

Réglage de la stabilité selon le type d’empennage

On utilise principalement trois variantes d’empennage horizontal dont la plus courante est l’empennage en croix (empennage horizontal en bas) dont l’efficacité ks varie environ de 0,4 à 0,6 en fonction de l’effet perturbateur du fuselage. Les empennages en T (empennage horizontal en haut de la dérive) ont une bien meilleure efficacité (ks ≈ 0,9) car ils sont au dessus du flux perturbé du fuselage. Mais leur principal avantage, surtout sur les planeurs, réside dans le fait que le stabilisateur est loin au dessus du sol, ce qui le protège lors des atterrissages sur terrain inégal. Certains sont adeptes des empennages en V, intermédiaire entre les deux précédentes solutions. Leur efficacité est celle des empennages en croix, mais il n’y a que deux surfaces au lieu de trois qui génèrent de la traînée.

Les interactions entre les axes

Chacun des trois axes d’un aéromodèle peut donc être caractérisé et réglé comme on vient de le voir. Malheureusement, toutes ces dispositions n’empêchent pas les axes d’interagir les uns avec les autres, pour le meilleur et pour le pire.

L’interaction la plus connue est le roulis induit. Si on donne du dièdre aux ailes, alors lorsqu’on agit sur la dérive, la rotation du modèle en lacet augmente l’incidence de l’aile extérieure au virage qui se lève et amplifie le virage ; on peut alors se passer d’ailerons. Cette technique de pilotage est considérée comme contre nature par certains, mais conserve des adeptes. Les frères Wright ont dès le début essayé de démontrer qu’un virage devait être obtenu par inclinaison des ailes et donc directement par une action en roulis.

Il est intéressant de noter que le système fonctionne de façon réciproque. Lorsque le modèle roule suite à une perturbation, les ailes tendent à glisser dans le sens de l’inclinaison, ce qui met le modèle en crabe à cause de l’empennage qui ne suit pas, puis entraîne dans un troisième temps l’accroissement de l’élévation de l’aile extérieure et une mise en virage incliné du modèle. On peut considérer que ça stabilise le modèle. Cet effet, aussi appelé « effet de dièdre », peut également être obtenu par des ailes en flèche ; 6° de flèche équivalent à environ 1° de dièdre. C’est pour cette raison que certains avions comme l’avion de transport militaire Lockheed Galaxy [4] (photo 2) ont un dièdre négatif pour compenser partiellement la forte flèche destinée à augmenter le nombre de Mach critique.

Photo 2 : Lockheed Galaxy. Noter la flèche et le dièdre inverse (photo Majalah Militer)

Une autre interaction très connue est le lacet inverse. Il est surtout sensible avec les ailes à grand allongement. L’aile intérieure au virage, aileron levé, subit moins de traînée que l’aile extérieure aileron baissé (voir polaires). Il s’en suit une rotation en lacet du modèle vers l’extérieur du virage qui impose une action de compensation sur la dérive vers l’intérieur du virage. C’est le traditionnel pilotage trois axes.

Un autre phénomène proche mais un peu moins connu mérite d’être expliqué. Lors des virages serrés, l’aile extérieure au virage voit une vitesse de flux d’air plus forte que l’aile intérieure qui a alors tendance à plonger et accentuer le virage. Il faut alors maintenir un ordre au manche légèrement vers l’extérieur du virage après qu’il ait été amorcé pour stabiliser le taux de virage.

Le roulis hollandais, moins souvent observé, résulte d’un couplage grave entre les axes de lacet et de roulis. Si un modèle a un dièdre important et une dérive peu amortie, une perturbation pour engendrer une oscillation en lacet qui en induit alors une en roulis et réciproquement. Le cercle vicieux amorce alors une oscillation mutuellement entretenue entre les deux axes qui peut finir en catastrophe.

Il existe d’autres couplages aérodynamiques et inertiels (liés à des moments d’inertie très différents selon les axes) qui ne sont pas développés ici. Ils se manifestent principalement sur les modèles à faible allongement et forte plage d’incidence, i.e. les modèles de jets. Ils peuvent conduire à la destruction d’un modèle car le pilote ne comprenant pas l’interaction entre les axes réagit à contre puis perd le contrôle. Plusieurs pilotes d’essais de haut niveau ont perdu la vie avant que ces interactions soient bien comprises…

Les modèles à empennage canard

La stabilité vient d’être étudiée dans le cas de la formule aérodynamique classique, c'est-à-dire celle avec un plan (les deux ailes) à l’avant et un stabilisateur en lacet et tangage à l’arrière. Il convient maintenant de considérer brièvement les particularités des autres formules.

La disposition « empennage à l’avant » dite empennage canard (photo 3), solution des frères Wright et de Dick Rutan, a peu d’adeptes. Pourtant, bien exploitée, elle fonctionne parfaitement.

Contrôle

Un avion à empennage canard se contrôle sur les trois axes comme un avion classique ; la seule différence notoire est que ces aéronefs ne décrochent en général pas ; ils se contentent de s’enfoncer si on tire trop sur le manche, mais reprennent une position de vol normale dès qu’on rend la main.

Equilibre et stabilité dynamique

Les équations d’équilibre et de stabilité se démontrent pour un empennage canard de la même façon que pour un empennage à l’arrière. Mais le centre de masse étant cette fois devant le foyer des ailes, les ailes sont un facteur stabilisant et le « stabilisateur » un facteur déstabilisant. L’empennage canard est en fait la pour assurer l’équilibre statique car ce sont les ailes décalées vers l’arrière qui procurent la stabilité dynamique. L’empennage canard doit donc être de dimension juste suffisante pour « porter » l’avant, mais rester suffisamment petit pour ne pas compromettre la stabilité dynamique. De plus, il doit décrocher avant les ailes pour éviter les décrochages et vrilles à plat. Alchimie délicate !

La solution consiste à prendre un empennage à fort allongement de façon à augmenter la pente de portance qui doit être si possible au moins égale à celle des ailes (voir photo 3) ; ainsi, si sa surface est bien choisie, lorsque l’incidence augmentera, il décrochera juste avant les ailes principales et provoquera une abattée prévenant le décrochage des ailes.

Le problème de la formule est que l’empennage, en général trop petit pour assurer un amortissement suffisant, impose l’utilisation d’ailes en flèche nettement plus amortissantes selon l’axe longitudinal que des ailes droites.

Enfin, on place souvent la dérive dédoublée aux saumons des ailes, afin de ne pas avoir à prolonger le fuselage vers l’arrière. Cette disposition permet de plus de placer le moteur en position arrière ; disposition qui améliore la finesse, car le souffle de l’hélice ne rend plus l’écoulement aérodynamique turbulent à l’avant du fuselage.

Photo 3 : avion de tourisme Long-EZ (prononcer easy) de Burt Rutan (photo wikipédia)

Les divers types d’ailes volantes

L’empennage est une surface qui génère de la trainée et impose un fuselage qui ajoute du poids et encore de la trainée. Les ingénieurs aéronautiques ont donc naturellement essayé d’éliminer cet appendice tout en conservant équilibre et stabilité. Le site web de Michael Möller [5] consacre une place significative à l’étude des ailes volantes. On y trouve, entre autres, comme ça a déjà été signalé, le logiciel Nurflügel qui calcule les distributions de Cz et tous les paramètres utiles pour concevoir une aile volante efficace.

Il y a deux solutions pour résoudre le problème de stabilité de l’aile volante :

Utilisation d’un profil autostable

Si on utilise des ailes avec un coefficient de moment de basculement Cm_0,25 positif (profil FAUVEL [6]), les ailes auront tendance à se cabrer spontanément. En conséquence, il faudra placer le centre de masse à l’avant du foyer des ailes afin de générer un moment égal, mais en sens inverse de celui des ailes : – Cm_0,25. Comme un centre de masse en avant du centre de poussée procure la stabilité dynamique, l’empennage devient inutile. C’est le principe des ailes volantes du type Fauvel (du nom de l’ingénieur français qui a développé cette formule). On peut voir sur la photo 4 une aile conçue par cet ingénieur. Comme cette formule ne garantit pas la stabilité en lacet, une dérive verticale reste donc a priori indispensable pour obtenir la stabilité selon l’axe de rotation vertical.

Photo 4 : aile volante réalisée par l’ingénieur Charles Fauvel (photo du site Nurflügel)

Un profil symétrique a un moment de basculement nul, une aile cambrée avec le creux de cambrure en dessous a une meilleure portance, mais un moment de basculement Cm_0,25 négatif. A contrario, un profil cambré en sens inverse (creux vers le haut) a une portance plus faible mais un moment de basculement Cm_0,25 positif et est dit « autostable ». Ceci étant, on peut obtenir le même résultat avec des ailes à volets en maintenant ces derniers légèrement braqués vers le haut.

La formule de Fauvel, bien que séduisante ne s’est jamais beaucoup développée car ce qu’on gagne en supprimant fuselage et empennage est perdu par les ailes moins performantes. De plus, le faible amortissement selon l’axe de tangage rend le pilotage délicat lorsqu’on augmente l’allongement des ailes.

Utilisation d’ailes en flèche vrillées

Les frères Horten [7] de nationalité allemande se sont attachés durant les années 1930 et 1940 à réaliser des ailes volantes utilisant un profil classique plus efficace qu’un profil autostable, mais sur des ailes en flèche dont l’incidence au saumon était plus faible qu’à l’emplanture. Avec cette disposition, le saumon des ailes vrillé crée un moment de basculement positif compensant le moment de basculement Cm_0,25 négatif du profil. Le logiciel Nurflügel a été écrit en particulier pour permettre l’optimisation de cette architecture, notamment le choix du profil, le réglage du vrillage et du calage des volets. L’utilisation du logiciel Nurflügel est développée dans un chapitre suivant. Les ailes des frères Horten (photo 5) ont été déclinées en nombreuses variantes dont la dernière, un chasseur à réaction, aurait pu donner du fil à retordre aux alliées si la seconde guerre mondiale avait durée quelques mois de plus.

Photo 5 : aile volante Ho-9 des frères Horten (source inconnue)

Un des avantages de cette formule sur celle de Fauvel est la possibilité de se passer de dérive, car en cas de rotation autour de l’axe vertical, la trainée de l’aile qui avance augmente tandis que celle de celle qui recule diminue, ce qui stabilise cet axe. Le problème résiduel de l’absence de dérive est le lacet inverse (terme explicité au paragraphe suivant) qui n’est plus contré en virage. Pour s’en sortir, les frères Horten ont choisi une portance distribuée en forme de cloche (fonction sinus³) obtenu par le vrillage adéquat des ailes à flèche marquée. Ainsi, les ailerons en bout d’ailes placés dans une zone à portance presque nulle à cause du vrillage négatif ne génèrent que très peu de lacet inverse. Enfin, la flèche, en plus de stabiliser l’axe de lacet, contribue significativement à l’amortissement longitudinal.

Ce type d’aile a de nombreux adeptes en modélisme, notamment pour la pente et le combat du fait de son extrême simplicité et robustesse (pas de fuselage ni de dérive à construire et susceptible de se casser). En aviation grandeur cette formule a suscité de nombreuses recherches et donné corps à de multiples prototypes avant de se matérialiser chez Northrop-Grummann avec le bombardier stratégique B2. Cet avion mérite quelques commentaires. La qualité recherchée dans ce cas précis était la furtivité améliorée par la suppression des surfaces verticales. Ce bombardier moderne s’écarte quelque peu du concept initial des frères Horten par le fait que le vrillage des ailes n’est plus utilisé, ceci afin d’améliorer la finesse. En conséquence, la stabilité en tangage comme en lacet sont perdues. En tangage, une stabilité artificielle est obtenue par des commandes de vol électriques (pilotage à travers un ordinateur), système de commande semblable à celui de tous les avions modernes hormis les avions de tourisme. En lacet, le même dispositif est utilisé, mais il a fallu ajouter des petits volets de bord de fuite dédoublés aux saumons d’aile. Ces volets s’ouvrent comme des mâchoires de crocodile orientées vers l’arrière d’un coté ou de l’autre pour freiner l’aile qui aurait tendance à avancer dans un mouvement autour de l’axe de lacet.

Il est au demeurant possible que cette formule soit celle de l’avenir puisque la NASA a étudié selon cette formule ce qui pourrait être le successeur de l’A380. Il s’agit d’une aile volante respectant le concept « Blended Wing Body » proche du concept Horten pouvant emporter 800 passagers (voir photo 6). Cette aile volante présenterait une trainée 15 % plus faible que celle d’un avion utilisant une formule classique, avec les économies en rapport.

Photo 6 : Maquette du BWB de la NASA (source wikipédia)

Les biplans et multi-plans

Tout le monde connait la formule du biplan classique (photo 1) largement utilisée en indoor et rendue célèbre par les chasseurs de la première guerre mondiale. Le fonctionnement et le contrôle sont identiques à celui des monoplans.

Au départ, les frères Wright ont utilisé la formule biplan pour permettre l’augmentation de la surface alaire sans augmenter de façon démesurée l’envergure des ailes tout en augmentant la rigidité des ailes minces grâce au haubanage. Au cours de la première guerre mondiale, la formule permettait de diminuer l’inertie en roulis (envergure plus faible), et donc d’obtenir des chasseurs plus vifs. Pour bien fonctionner, cette formule nécessite un bon réglage des surfaces portantes qui interagissent. Il est aussi possible de placer deux paires d’ailes en tandem, ce qui va être abordé dans la suite de ce chapitre. Dans les deux cas, les interactions entre les plans (paires d’ailes) doivent être soigneusement étudiées pour optimiser le fonctionnement et les réglages. Ceci va être fait en utilisant la soufflerie numérique 2D Javafoil de Martin Hepperle, qui est présentée dans un chapitre suivant pour ceux qui ne la connaissent pas.

Il est aussi possible d’utiliser plus que deux plans, ce qui va aussi être évoqué dans la suite de ce chapitre

Biplans classiques

Les biplans à ailes superposées se comportent et se contrôlent comme des modèles classiques. Ils sont plus vifs car leur inertie en lacet roulis est plus faible du fait de l’envergure réduite. Toutefois, pour que leur fonctionnement soit optimal, il faut que chaque plan supporte une charge alaire identique, mais aussi que le plan inférieur décroche un peu avant le plan supérieur pour conserver la stabilité en tangage. Ceci est obtenu par un réglage quelque peu subtil des plans exposé ici.

Observation

Deux plans symétriques identiques placés à une corde de distance juste l’un au-dessus de l’autre dans la soufflerie Javafoil permettent d’étudier le comportement aérodynamique du biplan classique.

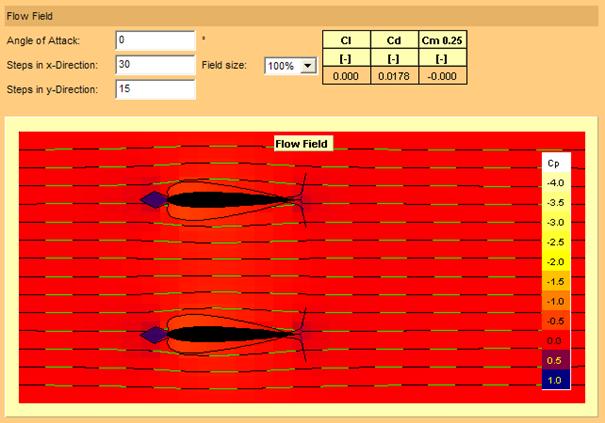
Figure 8 : profil symétrique biplan à incidence nulle

On peut observer sur la figure 8 que la section de passage est réduite entre les deux profils, et que l’air y est donc accéléré. C’est l’effet Venturi que l’on rencontre aussi dans la nature, en particulier dans les cols qui sont par conséquent très venteux. On peut aussi remarquer que la traînée de profil Cd = 0,0178 (Cd avec d pour drag correspond au Cx de la littérature française) est bien supérieure à celle observée dans le cas d’un monoplan.

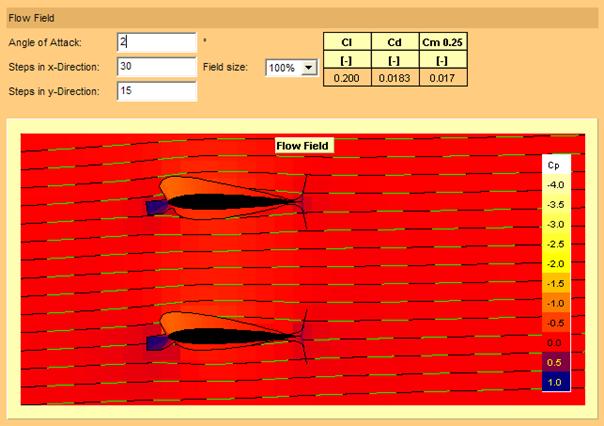
Figure 9 : profil symétrique biplan à incidence de deux degrés

A une incidence de deux degrés (figure 9) on note que la portance apparaît puisque Cl = 0,2 est positif (Cl avec l pour lift correspond au Cz de la littérature française) et que Cm_0,25 est positif ce qui dénote une tendance à cabrer. Dans la courbe de pression réduite Cp, les couleurs plus claires que le rouge dénotent un Cp (coefficient de pression) négatif, donc une dépression génératrice de portance. De la même façon, dans la courbe de pression réduite Cp, les couleurs plus sombres (mauves et bleues) dénotent une surpression, en l’occurrence en raison de leur orientation, essentiellement une traînée.

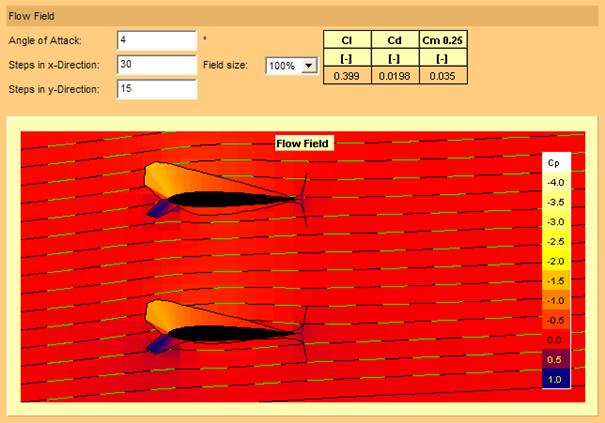
Figure 10 : profil symétrique biplan à incidence de quatre degrés

A une incidence de quatre degrés (figure 10) il apparaît nettement que la portance du profil inférieur est diminuée à cause de l’interaction avec le profil supérieur.

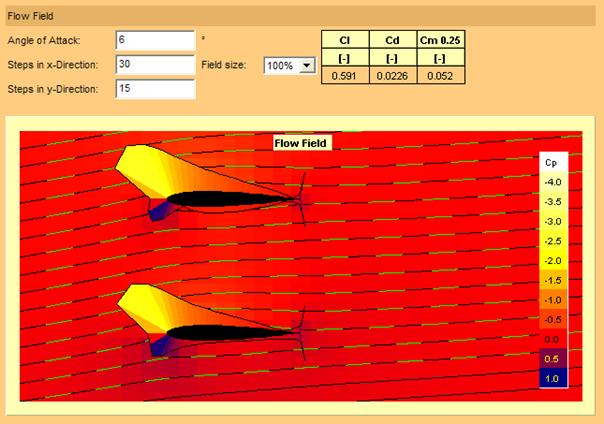
Figure 11 : profil symétrique biplan à incidence de six degrés

A une incidence de 6° (figure 11), le phénomène de masquage du profil inférieur est encore plus marqué.

Figure 12 : profil symétrique biplan à incidence de huit degrés

A huit degrés d’incidence (figure 12) on atteint enfin la portance Cl = 0,7 obtenue avec six degrés en monoplan, mais avec une traînée Cl = 0,0397 exactement double !

Analyse

Le fait que la portance est plus élevée sur le profil supérieur, implique que ce profil va décrocher en premier avec une triple conséquence :

• le profil inférieur restant seul porteur ne bénéficie que d’une stabilité longitudinale diminuée du fait de sa position sous le centre de gravité,
• la contrôlabilité en roulis disparaît si les ailerons sont uniquement sur le profil supérieur,
• la vitesse minimale est augmentée car c’est le décrochage du premier profil qui détermine la limite.

L’interaction des deux profils diminue donc l’efficacité du profil inférieur, ce qui détermine un décrochage prématuré et une perte de contrôlabilité du fait que le profil supérieur n’est plus opérationnel.

Optimisation

Pour un bon fonctionnement, il faudrait diminuer l’interaction entre les deux profils et faire en sorte que le profil inférieur décroche en premier. Ainsi seul, le profil supérieur contribuerait alors au vol après le premier décrochage avec une stabilité longitudinale augmentée par la position haute de ce profil et une contrôlabilité en roulis maintenue si les ailerons sont placés sur le profil supérieur.

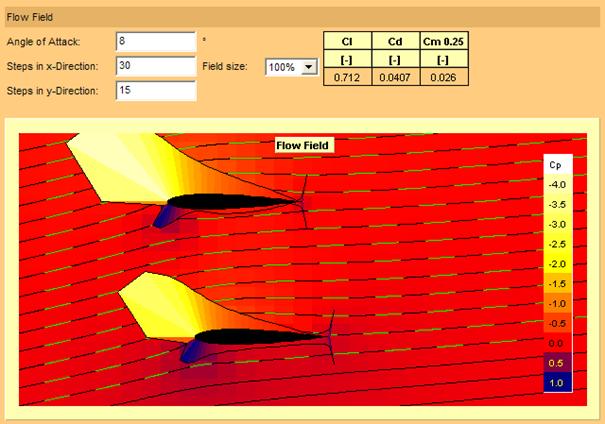
Figure 13 : recul du profil inférieur

Dans le cas de la figure 13 on a reculé le profil inférieur d’une longueur de 20 % de corde. On peut alors observer une augmentation de Cl, témoin de la diminution de l’interaction entre les deux ailes.

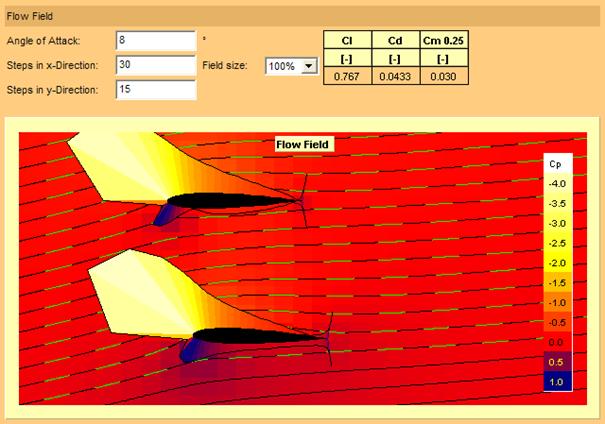
Figure 14 : pincement de 1.5°

Dans le cas de la figure 14 on a en plus du recul augmenté l’incidence relative du profil inférieur de 1,5° (pincement). Ce profil porte maintenant légèrement plus que le profil supérieur.

Tout est donc maintenant rentré en ordre, simplement par un recul du profil inférieur et un pincement. Il n’en reste pas moins vrai que la traînée est supérieure à celle de la formule monoplan, mais il ne faut pas oublier que le traînée induite n’est pas considérée ici, et elle est plus faible dans le cas d’une formule « biplan » du fait de l’allongement relatif double de chaque plan.

Deux plans en tandem

On peut aussi utiliser deux paires d’ailes en tandem, solution retenue sur le « Pou du ciel » de Henri Mignet [8] (photo 7) et dans un passé plus récent par Dick Rutan [9] avec la série des Quickie (photo 8). Mais gare à l’interaction entre les deux ailes qui est source de nombreuses difficultés et désappointements. Pour comprendre les interactions et s’en prémunir on aura tout intérêt ─ comme dans le cas du biplan traditionnel ─ à faire des simulations avec l’ensemble des surfaces portantes sous JavaFoil.

Le Pou du ciel est un deux axes, ce qui signifie qu’on tourne uniquement à la dérive grâce au roulis induit. Le contrôle en profondeur, quant à lui, est obtenu en faisant varier l’incidence des ailes avant. Comme les avions à empennage canard il ne décroche pas, mais se contente de faire une abatée si on tire trop fort sur le manche. Le système est très simple, ce qui a fait son succès, mais il est bien sûr hors de question de faire de l’acrobatie avec ce type de modèle.

Le Pou du ciel ─ initialement l’avion de « l’aviation populaire » française des années 30 ─ a été momentanément interdit de vol car plusieurs pilotes se sont tués à ses commandes. Dans certaines conditions, il devenait incontrôlable et passait sur le dos. La cause semble avoir été un mauvais choix de la position du centre de masse doublé d’un mauvais calage relatif des ailes. Ce défaut était facile à corriger, mais les accidents spectaculaires ont défrayé la chronique et temporairement discrédité l’avion. A l’époque il n’y avait pas d’ordinateur ni simulateur pour trouver la position idéale du centre de masse en tenant compte des interactions…

Photo 7 : Pou du ciel de Henri Mignet (photo association Pionnair de Genève)

Les Quickie de Burt Rutan reprennent le même concept que le Pou du ciel, mais cette fois les deux plans sont plus écartés, les ailes avant possèdent des gouvernes de profondeur tandis que les ailes arrières possèdent des ailerons classiques. Le pilotage est donc cette fois-ci traditionnel, si ce n’est que la commande de profondeur agit sur les ailes avant comme sur la formule canard. Comme pour la formule canard il n’y a pas de décrochage.

On pourra remarquer que Burt Rutan a préféré par la suite la formule canard à la formule biplan en tandem car les interactions entre les deux paires d’ailes contrarient l’optimisation aérodynamique. Ce type d’avion de tourisme reste toutefois toujours fabriqué, même s’il reste marginal, car comme son nom le suggère il est très rapide.

Photo 8 : Biplan en tandem Quickie II de Burt Rutan (photo wikipédia)

Que les deux plans soient superposés ou en tandem, ils interagissent. Comme dans le cas des biplans classiques, l’étude des interactions avec la soufflerie numérique Javafoil se justifie et est présentée ci-après.

Dans cette étude on place les deux mêmes profils que précédemment l’un derrière l’autre à trois cordes de distance.

Observation

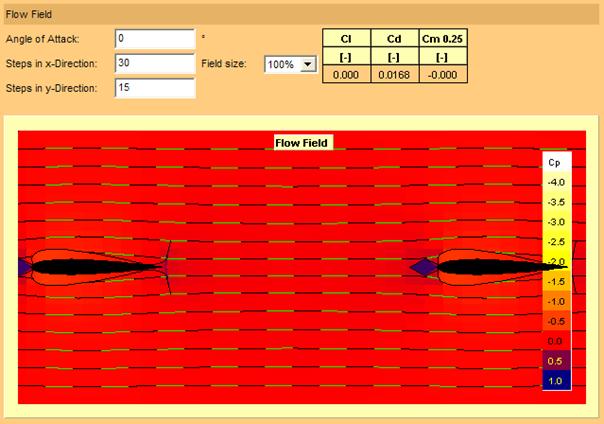
Figure 15 : deux profils en tandem

Dans la figure 15 on observe que comme dans le cas du biplan la traînée de profil est nettement plus forte que dans le cas d’un monoplan.

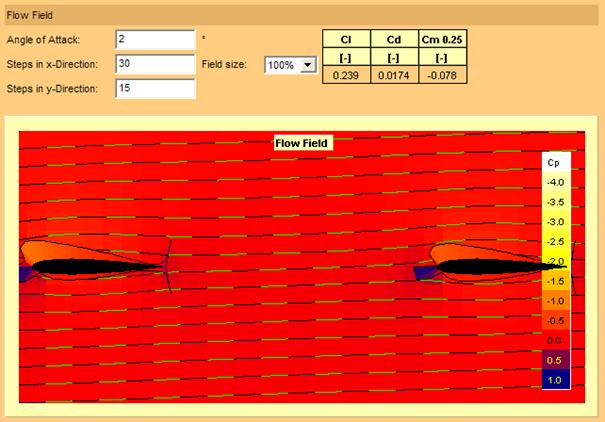
Figure 16 : incidence de deux degrés

R. A. S. dans la figure 16 placée ici pour mémoire.

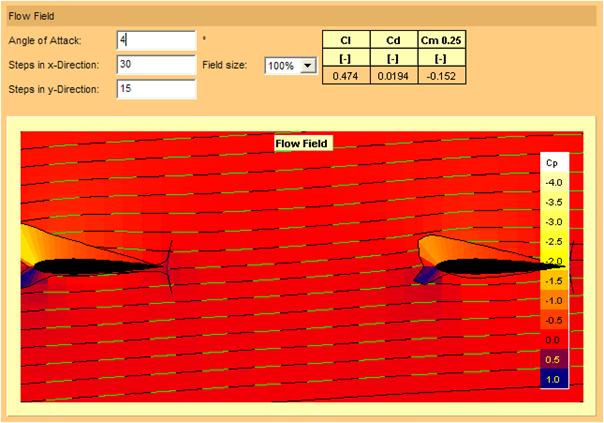
Figure 17 : incidence de quatre degrés

On observe figure 17 que le profil arrière devient moins porteur que le profil avant ce qui induit un autocabrage.

Figure 18 : incidence de 6°

La figure 18 met en évidence une perte de portance globale négligeable par rapport à la solution monoplan à une incidence de 6°. En effet, Cl descend de 0,7 à 0,686. Cependant, faute d’empennage, le système n’est a priori pas stable et la perte de portance du plan arrière est gênante.

Analyse

L’interaction entre les deux profils diminue l’efficacité du profil arrière qui décrochera après le profil avant. L’optimisation est beaucoup plus difficile que dans le cas du biplan classique car on ne dispose pas d’empennage pour garantir la stabilité.

La figure 15, au demeurant, met en évidence le problème qui affectait les « Poux du ciel » et ont contribué à son discrédit. On voit en effet que la portance part vers le profil avant lorsque l’incidence augmente et donc que l’on ralentit, ce qui induit un autocabrage jusqu’à ce que le profil avant décroche. L’aéronef pique alors, accélère et le profil arrière ─ seul porteur ─ fait passer l’engin cul par-dessus tête. Analyse à la mémoire des pilotes de Poux qui se sont tués comme ça…

Optimisation

Tel que présenté, le système « tandem » n’étant a priori pas stable longitudinalement il convient de diminuer l’incidence du profil arrière en diminuant son incidence d’environ 1,5° comme dans le cas de la figure 19.

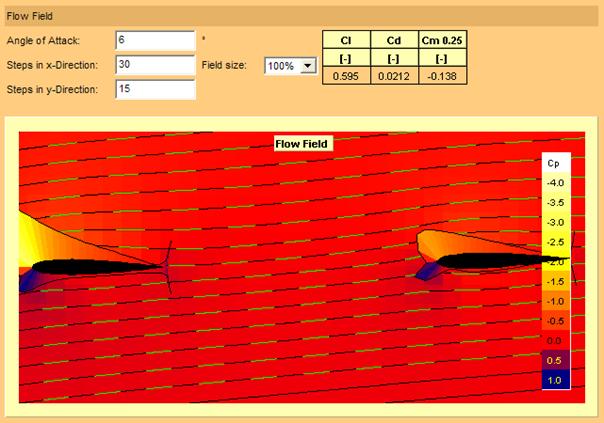
Figure 19 : pincement de 1,5°

Cette fois (figure 19), le système est stable, mais la perte d’efficacité du profil arrière fait que le coefficient de portance chute de 0,7 à 0,595 par rapport à la solution « monoplan ». Le système est donc peu performant en termes de portance.

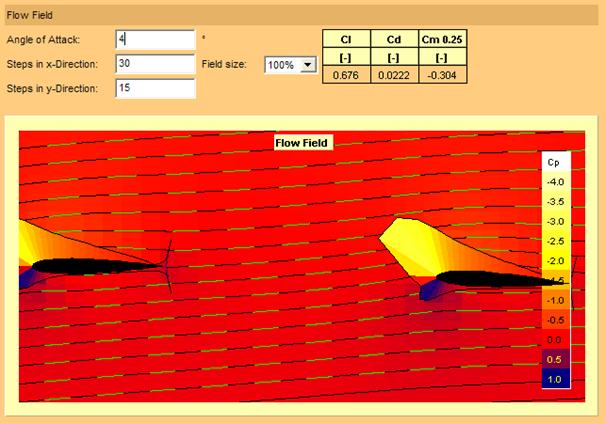
Figure 20 : pincement négatif de 4°

Avec un pincement négatif de quatre degrés (figure 20) la portance est plus que rétablie, mais le système est cette fois instable longitudinalement ! Cette solution est donc exclue et explique pourquoi Burt Rutan a finalement basculé vers la solution « canard ».

Plus de deux plans

Hormis les triplans de la première guerre mondiale qui ne sont que des variantes des biplans et les sextiplans qui sont eux des biplans avec des ailes inférieures réduites, on a pu voir apparaitre ça et là des avions avec encore plus de plans. Le record appartient au Caproni Ca.60 (photo 9) qui n’en comptait pas moins de 9 mais qui n’a pas volé ; avis aux maquettistes fondus de construction d’ailes !

Photo 9 : hydravion italien Caproni Ca.60 (photo de vidéo Youtube)

Les configurations inhabituelles

Le premier « Avion »

Pour des questions d’image, chaque pays aimerait avoir le premier homme qui a volé, même si à l’époque des premiers exploits aucun gouvernement n’a rien financé dans ce domaine à l’exception notoire de l’armée française qui a financé, mais sans succès, l’Avion III de Clément Ader, le terme « Avion » étant au demeurant une invention de M. Ader. Objectivement, la victoire est un effort combiné puisque l’allemand Lilienthal est le premier à avoir réussi des vols planés contrôlés (sans sa mort accidentelle il aurait certainement été le premier) et son expérience a servi aux suivants ; en particulier aux frères Wright qui ont réussi le vrai premier vol motorisé contrôlé. Malheureusement pour eux, leur formule aérodynamique canard mal optimisée a coûté la vie du militaire qui aurait dû leur faire accorder le soutien de l’armée américaine ; ils n’ont donc droit qu’à une demi victoire (c’est entre-autre la raison pour laquelle ils se sont réorientés vers la construction de moteurs d’avion). Puisque les américains n’ont droit qu’à une demi-victoire il faut accorder un peu de victoire à d’autres, en particulier au brésilien Santos Dumont qui a réussi à voler un peu plus tard indépendamment des frères Wright (les informations circulaient mal à l’époque) et qui a lui le mérite d’avoir produit la « Demoiselle », premier avion vraiment opérationnel qui a été fabriqué en plusieurs exemplaires. Blériot sauve l’honneur français en ayant été le premier à aller d’un endroit à un autre choisi à l’avance sans possibilité de changer d’avis (sauf à se décider à nager…). La France serait définitivement gagnante de ce duel si Ader avait produit quelque chose d’utilisable. Il ne reste donc qu’à le démontrer.

Indiscutablement, les deux avions d’Ader (Avion I alias Eole et Avion III) n’ont pas permis de vol contrôlé, et Clément Ader a surtout essayé d’imiter les chauves souris sans résoudre les problèmes de contrôlabilité et stabilité ; M. Ader n’étant pas très porté sur la recherche d’antériorité et l’analyse du travail des autres.

Heureusement, Alain Vassel va sauver l’honneur de la France en réalisant une maquette de l’Eole (photo 10) ─ le premier avion d’Ader ─ et en démontrant qu’elle peut voler. Mais attention : l’honnêteté intellectuelle oblige à avouer qu’il a fallu modifier certains de ses paramètres fondamentaux ; Alain Vassel insistant sur le fait que ses essais ont surtout démontré (comme il a été précisé au début du chapitre) que l’Avion I ne pouvait pas voler tel qu’il était conçu initialement [2].

N. B. : Alain Vassel a aussi réalisé une magnifique maquette de l’Avion III, mais qui n’a pas volé.

Photo 10 : maquette de l’Eole par Alain Vassel (photo Alain Vassel)

Comme on peut le voir sur la photo, il n’y a pas d’empennage et le profil très creux est aussi très instable. Ce qui rend le vol possible, c’est le centre de masse de la maquette très en-dessous des ailes qui compense tout juste l’instabilité aérodynamique. Selon les propres propos d’Alain Vassel, lorsque le modèle est parfaitement réglé il peut s’élever et progresser en ligne droite, mais le réglage, critique, varie d’un vol à l’autre car l’ensemble est très flexible. En fait, Ader avait prévu la possibilité de modifier la forme des ailes à l’aide de six manivelles. Ceci permettait à défaut d’un réel pilotage, au moins de régler parfaitement la position du centre de poussée des ailes.

Stabilisateur devant et derrière

On peut utiliser un stabilisateur devant et un autre derrière comme sur le X29 [10] (photo 11) ou le Pushy Galore [11] (photo 12). La logique qui conduit à cette solution peut paraître obscure de prime abord, mais on comprend mieux si on sait que l’empennage avant sert avant tout à l’équilibre statique en compensant le couple piqueur de l’aile, qui grâce à ces « moustaches » peut adopter un profil beaucoup plus porteur (solution adoptée sur la majorité des ailes delta modernes) ; l’empennage arrière servant, quant à lui, à donner l’amortissement et la manœuvrabilité nécessaires.

Dans le cas du X29, le plus visible est la flèche inverse, mais c’est une innovation indépendante de celle du double contrôle ; le prototype en incluant d’ailleurs aussi d’autres comme les ailes à galbe variable dynamiquement. Qui osera en faire une maquette conforme ?

Photo 11 : avion expérimental Grumman X29. Noter les empennages avant et arrière. (photo wikipédia)

Photo 12 : avion de course F1 « Pushy Galore ». Noter les empennages avant et arrière (photo Airventure Museum)

Le cas de l’hélicoptère

Comme pour les autres aéronefs, on va s’intéresser au contrôle et à la stabilité des modèles d’hélicoptères. Cela va obliger à rappeler quelques principes de base de ce type d’aéromodèle, mais ceci n’étant pas l’objet principal du paragraphe, ces principes généraux ne seront pas approfondis.

Principe de base de l’hélicoptère

L’idée de base de l’hélicoptère est d’utiliser une hélice nommée « rotor » dans ce cadre en position verticale pour créer une portance, même à vitesse horizontale nulle. Afin de rendre l’engin contrôlable, on fait varier de façon cyclique le pas de ce rotor. Le terme « cyclique » signifie : faire en sorte que le pas dépende de la position angulaire des pales. Par exemple : pour aller vers l’avant on augmente le pas à l’arrière de l’hélicoptère et on le diminue à l’avant, ce qui fait basculer l’aéronef vers l’avant et donc avancer. Pour mettre l’hélicoptère en virage il faut l’incliner à l’intérieur de la courbe, ce qui s’obtient en augmentant le pas du coté extérieur au virage et en le diminuant du coté intérieur. Pour contrer le couple de rotation généré par la trainée des pales on ajoute soit un rotor secondaire d’anticouple placé verticalement dans la queue, soit on utilise deux rotors contrarotatifs. Ce dispositif supplémentaire permet contrôle en lacet.

Le principe de base de l’hélicoptère est simple mais pose de nombreux problèmes de stabilité :

· Dans le sens vertical le comportement est stable dans l’effet de sol, mais neutre en hauteur,

· le contrôle en lacet est très difficile du fait d’une faible inertie selon cet axe et une stabilité neutre,

· l’hélicoptère n’est pas très stable en roulis comme en tangage, et même une très faible inclinaison provoque rapidement une dérive s’accélérant d’un coté ou d’un autre.

Les deux formules principales

Solution avec rotor anti-couple

La solution la plus classique pour résoudre le problème du couple généré par le rotor de sustentation appelé ici principal est d’ajouter un rotor secondaire de queue placé dans un plan vertical et destiné à compenser ce couple (voir photo 13). Il est en général entrainé par le moteur de sustentation via un réducteur mécanique. De cette manière toute variation de la vitesse de rotation du rotor principal entraine instantanément une variation proportionnelle de celle du rotor de queue. Pour contrôler l’hélicoptère en lacet il suffit alors d’augmenter ou diminuer le pas des pales du rotor de queue selon le sens de rotation désiré.

Photo 13 : hélicoptère électrique à formule classique Trex 450 (photo Société Align)

Le rotor de queue de certains petits hélicoptères indoor est directement contrôlé par un moteur électrique autonome. Ce système est mécaniquement plus simple, mais l’inertie du rotor de ce moteur qui crée un temps de latence à l’accélération rend le pilotage moins précis.

Formule birotor

La formule birotor coaxiaux est très en vogue pour les modèles indoor de début (voir photo 14). Dans ce cas, l’axe du rotor est double, constitué d’un axe interne qui entraine le rotor du haut, et d’un axe externe creux entrainant le rotor du bas. Dans cette disposition chaque axe est entrainé en sens inverse par un moteur indépendant. Pour contrôler l’axe de lacet il suffit d’appliquer une vitesse différentielle entre les deux moteurs (on fait varier la vitesse relative d’un moteur par rapport à l’autre).

Photo 14 : hélicoptère indoor Lama à rotors contrarotatifs (photo Esky)

Les hélicoptères grandeur utilisent parfois deux rotors indépendants placés en tandem.. Cette formule d’un fonctionnement très semblable à celui de la formule coaxiale n’est retenue en modélisme que dans le cadre maquette. On trouve aussi plus rarement la solution avec deux rotors côte à côte.

Le pilotage

Le pilotage d’un hélicoptère est assez semblable à celui d’un avion avec une différence majeure : la puissance du moteur génère un mouvement vertical au lieu d’un mouvement horizontal vers l’avant. De plus, l’hélicoptère possède deux régimes de vol :

· Le vol stationnaire durant lequel l’hélicoptère n’évolue qu’à très faible vitesse sans s’incliner de façon significative.

· Le vol de translation durant lequel l’hélicoptère évolue à vitesse horizontale soutenue et se comporte comme un avion.

Le contrôle dans les deux domaines peut se faire avec une radiocommande classique à deux manches et quatre axes de commande.

Les quatre axes de commande

· Le premier axe de commande correspond aux gaz d’un aéromodèle à voilure fixe. Le but de cet axe est de contrôler la vitesse de montée et descente. Ici, on agit en général simultanément sur le pas collectif (variation simultanée du pas de chaque pale indépendamment de leur position angulaire) et les gaz de façon à maintenir à peu près constant le régime de rotation du rotor. Dans le cas d’une propulsion électrique on utilise parfois un variateur à régulateur de vitesse intégré qui garantit un régime de rotation parfaitement fixe du rotor de sustentation. Dans le cas de petits hélicoptères indoor le réglage du pas collectif est parfois absent (hélicoptères dit FP) et on contrôle alors la montée et la descente uniquement aux gaz.

· Le second axe est l’axe de lacet, correspondant à celui de la dérive d’un aéromodèle à voilure fixe. Dans le cas de l’hélicoptère c’est un axe très sollicité, fondamental en stationnaire où il détermine le contrôle de cap. L’action se fait sur le pas (ou éventuellement le régime) du rotor de queue ; soit dans le cas de la formule birotor sur le régime (ou pas différentiel) des deux rotors de sustentation.

· Le troisième axe est le contrôle de pas cyclique avant/arrière qui permet d’incliner l’hélicoptère vers l’avant pour contrôler l’avancement en translation.

· Le dernier axe est le contrôle de pas cyclique latéral pour incliner l’hélicoptère afin de le mettre en virage lorsqu’on est en régime de translation.

Le problème de la stabilité

Stabilité en montée et descente

Le contrôle des gaz permet dans l’effet de sol (environ une hauteur d’hélicoptère) de régler la hauteur de l’aéromodèle, mais au-delà, les gaz devront en permanence être retouchés pour conserver une hauteur constante. Il s’agit d’un cas typique de stabilité neutre qui nécessite un bon apprentissage. Les corrections doivent être très fréquentes pour rester petites, ce qui nécessite d’entrainer la vue comme les doigts.

Selon cet axe, la variation de pas est nettement préférée à la variation de régime, car l’inertie à l’accélération qui induit un temps de réponse rend le contrôle plus ardu dans le cas d’un régime variable.

Stabilité en lacet

Si la stabilité est neutre selon la direction verticale, elle l’est aussi selon l’axe de lacet, avec comme problème supplémentaire une faible inertie selon cet axe ; sans compter que de nombreux facteurs externes perturbent cet axe.

Les hélicoptères grandeur ont suffisamment d’inertie pour que cet axe soit normalement contrôlable, mais dans le cas de nos modèles réduits, le contrôle est très difficile et on ajoute toujours un artifice de stabilisation nommé gyroscope. Ce dispositif est aujourd’hui en réalité un gyromètre, c'est-à-dire un capteur détectant les vitesses de rotation autour de l’axe vertical, couplé à une électronique agissant sur le rotor de queue (ou le différentiel d’un rotor contrarotatif) afin de maintenir la vitesse de changement de cap de l’hélicoptère nulle, ou fixée à une valeur proportionnelle à l’ordre de rotation.

On appelle ce type dispositif « un asservissement » car on asservit l’action (ici l’action sur l’axe de lacet) à la mesure (ici la mesure de vitesse de rotation en lacet). Avec ce type de système l’action sur la gouverne à partir du manche de commande est indirecte car le manche donne uniquement une consigne de vitesse de rotation et c’est le système capteur plus électronique qui génère la commande adaptée. On notera qu’un servo (abréviation de servomoteur) est aussi un asservissement, car lorsqu’on donne un ordre au manche, le moteur du servo tourne jusqu’à ce que le potentiomètre du servo (capteur angulaire) recopie l’angle demandé par l’inclinaison du manche. Les asservissements sont très utilisés, car ils permettent, entre autres, de rendre stable un système naturellement instable. Les avions de ligne et de combat sont tous aujourd’hui contrôlés par des « commandes de vol électriques » qui sont ni plus ni moins que des asservissements. Le Concorde anglo-français a été le premier avion civil disposant de ce perfectionnement. En maquettisme ces dispositifs sont interdits, même si on reproduit un aéronef qui en était doté !

Dans le cas des modèles réduits d’hélicoptère les gyroscopes peuvent fonctionner selon deux modes :

· mode normal où on cherche à limiter la vitesse parasite de rotation en lacet,

· mode « heading lock » (verrouillage de cap) qui tend à limiter la dérive par rapport au cap de consigne.

Stabilité en roulis et tangage

Si l’hélicoptère n’est stable ni verticalement ni en lacet, il ne l’est guère non plus et roulis et tangage. En fait, l’hélicoptère pourrait être suffisamment stable selon ces deux axes si le rotor était situé plus haut au-dessus de la cabine ; certains hélicoptères indoor utilisent d’ailleurs cette astuce (voir photo 14). Les hélicoptères RC utilisent depuis longtemps un asservissement mécanique assez compliqué pour stabiliser ces deux axes (photo 15) appelé système « Bell-Hiller », du nom des sociétés qui ont introduit la barre inertielle (dite de Bell) puis les palettes de commande (dites de Hiller).

Photo 15 : tête de rotor avec stabilisateur Bell-Hiller (photo Align)

La barre de Bell (flybar en anglais) est une barre avec deux masselottes (visible sur la photo 13) qui fait office de gyroscope et qui commande directement le pas cyclique. Comme tout gyroscope, sa position est stabilisée dans l’espace, donc si l’hélicoptère s’incline par rapport à son plan de référence, les leviers reliant la barre aux pales introduisent un changement de pas correcteur. Dans la variante de Hiller ─ presque toujours utilisée sur nos modèles RC ─ des palettes aérodynamiques sont ajoutées en bout de barre, et lorsqu’on agit sur le pas cyclique, on le fait via les palettes. Un ordre en roulis ou tangage fait tourner la barre sur elle-même, ce qui incline les palettes, puis par réaction aérodynamique fait basculer la barre qui finalement fait changer de façon cyclique le pas des pales.

Ceci étant, on commence à voir des asservissements électroniques à un prix raisonnable appelés systèmes « flybar less » (sans barre inertielle) ou « Virtual Flybar » pour remplacer cet asservissement mécanique. On trouve même chez Robbe un système, un peu cher, capable d’asservir un hélicoptère en attitude et position car il observe le sol à l’aide d’une caméra. La stabilisation électronique, système, relativement nouveau, devrait donc remplacer petit à petit le système compliqué actuel de chapes, leviers et barres.

Les réglages

Tout comme les modèles à voilure fixe, les modèles à voilure tournante nécessitent un certain nombre de réglages abordés brièvement ici.

Calage des pales

Le contrôle des hélicoptères se fait le plus souvent par variation du pas des pales du rotor. Aussi lorsqu’aucune action en roulis ou tangage n’est initiée, les deux pales doivent avoir le même pas. Si ce n’est pas le cas, une pale fléchit plus que l’autre, ce qui peut se voir en observant les deux cercles décrits par chaque pale. Une très mauvaise idée consiste à mette ses yeux à hauteur des pales pour mieux voir le décalage car il arrive que la force centrifuge arrache une pale (ce n’est pas une plaisanterie). Ce réglage appelé « réglage du tracking » doit donc se faire de préférence à deux en prenant des précautions de sécurité.

Réglage du gyroscope

Les asservissements de nos petits gyroscopes (voir photo 16) sont en général très primitifs. Aussi, pour que leur fonctionnement soit satisfaisant, il faut les régler.

Photo 16 : gyroscope de queue : noter les deux trous ronds pour le réglage (photo Ikarus)

Le premier réglage est le calage du zéro, c'est-à-dire du pas du rotor de queue lorsqu’aucune action en lacet n’est initiée. Si ce réglage n’est pas bon, l’hélicoptère aura tendance à toujours tourner d’un coté ou de l’autre. Il faut aussi régler le gain. Lorsque le gain est nul il n’y a pas d’asservissement. Plus le gain est fort, plus l’asservissement est efficace, mais lorsque le gain est trop fort le système a tendance à osciller. Le réglage consiste donc à augmenter le gain petit à petit jusqu’à l’observation des oscillations, puis de revenir un peu en arrière.

Pour qu’un gyroscope soit parfaitement réglé, il faut d’abord le laisser chauffer quelques minutes (nos gyroscopes primitifs dérivent avec la température) puis faire plusieurs fois de suite alternativement le réglage du zéro et du gain.

Choix des débattements

Si le comportement d’un avion dépend de sa forme, de la taille de ses gouvernes, etc., le comportement d’un hélicoptère dépend lui essentiellement du débattement des commandes sur chaque axe et des caractéristiques de sa barre de Bell-Hiller.

Un débutant choisira donc un débattement limité avec peu de débattement vers le bas pour le pas collectif, alors que pour faire de l’acrobatie, les débattements seront augmentés et le débattement du pas collectif sera symétrique par rapport au neutre.

Réglage de la stabilité en roulis et tangage

Le réglage de la barre de Bell-Hiller faite par le fabricant de l’hélicoptère donne en général satisfaction et il n’est pas recommandé d’y toucher sans savoir ce que l’on fait. Toutefois, il arrive qu’au bout d’un certain temps on ait envie de changer quelque peu le comportement de son hélicoptère, le plus souvent pour le rendre plus réactif afin de tenir compte de ses progrès en pilotage. Le réglage de stabilité se fait en réglant les poids des masselottes (ou éventuellement des palettes) ; plus les masselottes seront lourdes, plus l’hélicoptère est stable. Le réglage du contrôle se fait par les palettes ; plus les palettes sont grandes, plus la commande est efficace. Pour débuter on préfèrera donc de grosses masselottes et des petites palettes. Pour améliorer la vivacité il est aussi possible de jouer sur les deux anneaux amortisseurs placés entre la tige porte pales et la tête de rotor ; mais cette action est plus délicate à mener.

Références

1. Clément Ader (wikipédia)
2. Site d’Alain Vassel, Epilogue sur Clément Ader
3. Les frères Wright (wikipédia)
4. Avion de transport Lockheed Galaxy (wikipédia)
5. Site web sur ailes volantes (Michael Möller)
6. Biographie de Charles Fauvel
7. Biographie des Frères Horten (site aerostories)
8. Henri Mignet (Association Pionnair)
9. Burt Rutan (wikipédia)
10. Avion expérimental X29 (wikipédia)
11. Avion de course F1 « Pushy Galore » (Airventure Museum)