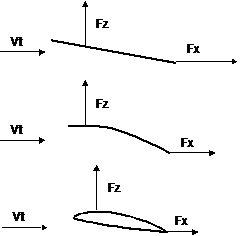Calculer son modèle réduit

L’aérodynamique définit le comportement en vol des aéronefs (avions et aéromodèles). Ce chapitre est donc essentiel ; de nombreux autres chapitres de cet ouvrage dépendant des concepts développés dans ce chapitre.

L’aérodynamique est une science appliquée complexe qui a été approfondie à partir des premiers vols humains entre la fin du XIX^ème siècle et l’aube de XX^ème, mais qui n’a été complètement maitrisée qu’une soixantaine d’années plus tard quand sortaient des usines les premiers avions de transports transsoniques (BOEING 707, CARAVELLE…) et CONCORDE. Dans les années 1950 il subsistait encore de nombreuses petites imperfections dans les avions dues à une connaissance imparfaite de l’aérodynamique. Afin d’établir la chronologie des progrès en aérodynamique, ce chapitre va commencer par un bref historique.

Histoire des progrès de l’aérodynamique

Seuls les points clefs des progrès de l’aérodynamique vont être mis en exergue ici ; une histoire beaucoup plus complète de l’aérodynamique étant présentée dans l’ouvrage de John D. Anderson Jr [1].

L’aérodynamique est une partie d’une science plus générale : la dynamique des fluides. Cette science fondamentale a été étudiée bien avant le premier vol. Léonard de Vinci avait déjà montré au XV^ème siècle que la traînée d’un corps (voir la définition plus loin dans ce chapitre) était proportionnelle à sa section maîtresse (maître couple). Galilée un siècle plus tard avait non seulement découvert les satellites de Jupiter qui lui ont valu ses ennuis avec l’Inquisition mais aussi que la traînée était proportionnelle à la densité du fluide dans lequel baignait le corps étudié. Newton a au XVII^ème parachevé les équations de base de la mécanique des fluides en montrant que la traînée était proportionnelle au carré de la vitesse. Plus fort, les équations de Bernoulli comme celles de Laplace qui définissent sous forme d’équations différentielles le comportement de tout fluide incompressible non visqueux étaient connues au XVIII^ème siècle. Le travail théorique était parachevé dès 1840 par Navier et Stokes qui ont résolu le problème plus général des fluides visqueux, mais on n’a pu en tirer profit qu’après 1960 avec le développement des ordinateurs de calcul scientifique…

Clément Ader, considéré en France par beaucoup comme le premier homme ayant volé, était plus justement le dernier à essayer de le faire de façon principalement empirique. Ce fût un échec pour de nombreuses raisons, conséquences d’une approche non scientifique. Une étude très poussée et complète diffusée sur Internet, menée sur de nombreuses années avec plusieurs maquettes à l’appui, faite par Alain Vassel [2] démontre sans équivoque que Clément Ader n’a jamais réussi à voler, et que le mythe n’a été entretenu que pour des questions d’orgueil national mal placé.

Lilienthal est beaucoup plus sûrement le vrai précurseur de l’aviation, car à l’opposé d’Ader il avait lui une démarche scientifique s’appuyant sur les connaissances théoriques de l’époque et calculant tout ce qui était possible. On lui doit les premières polaires d’aile (méthode de représentation des caractéristiques aérodynamiques inventée par lui même) et les premières études de stabilité et de contrôlabilité. Il est de facto le premier humain ayant quitté le sol avec un "plus lourd que l’air" contrôlé, même si ce n’était qu’en vol plané. Il s’est malheureusement tué au cours d’un de ses très nombreux vols en découvrant le décrochage…

Les frères Wright ont repris les écrits et méthodes de Lilienthal et se sont aperçu que ses polaires étaient fausses. En fait, celles des frères Wright étaient fausses aussi car les mesures étaient faites sur des maquettes à petite échelle dont le comportement était différent à cause du facteur d’échelle : le nombre de Reynolds déjà connu, mais qui ne sera appliqué que bien plus tard aux profils. Ceci étant écrit, Lilienthal avait déjà justement remarqué qu’une aile galbée portait mieux qu’une aile plane et Langley (le concurrent direct malheureux des frères Wright) avait noté que des ailes allongées traînaient moins que celles à faible allongement, découvertes que les frères Wright ont mis à profit dans leurs "flyers" successifs. Mais l’apport principal des frères Wright vient de l’invention des surfaces de contrôle. Lilienthal contrôlait ses planeurs en déplaçant le centre de masse comme sur les ailes delta, alors que les frères Wright ont inventé le gauchissement des ailes et les empennages mobiles.

Les frères Wright ont de plus été les premiers à montrer que pour virer il fallait incliner l’aéroplane comme un vélo, le virage à plat comme une voiture à la dérive étant une erreur. Le gauchissement des ailes, étape fondamentale dans la méthode de contrôle en roulis était encore en usage sur de nombreux aéroplanes du début de la première guerre mondiale, mais a été rapidement remplacée par des ailes rigides associées à des gouvernes mobiles baptisées "ailerons". Le Blériot XI qui a le premier traversé la manche utilisait encore la méthode du gauchissement. Mais on doit préciser à l’intention des maquettistes que pour virer, le gauchissement seul n’était pas suffisamment efficace ; il fallait impérativement y ajouter la dérive pour profiter du roulis induit. Toutes les vraies maquettes d’avions de cette époque (celles où on ne triche pas sur les dimensions) sont donc délicates à piloter, et ceci d’autant plus que le centrage était souvent limite arrière (impossible de tricher le plus souvent à cause de la position du train d’atterrissage) et que les surfaces d’empennage étaient très petites. Les corrections sur ces avions devaient être incessantes et très précises (témoignage d’un pilote de réplique de Blériot XI).

La guerre est un formidable moteur de progrès technique. On doit à la première guerre mondiale les premiers avions réellement efficaces. Des laboratoires d’étude aérodynamique se sont développés en Grande Bretagne (RAAF), aux USA (NACA) et en Allemagne (laboratoires de Göttingen), et c’est à ceux de Göttingen que l’on doit l’invention de l’aile épaisse en 1917. On s’aperçoit alors que l’épaisseur du profil augmente un peu la traînée, mais significativement la portance, d’où la possibilité avec une aile épaisse de diminuer la surface et donc la traînée tout en augmentant la rigidité. Le premier avion à bénéficier de cette découverte a été le Fokker triplan DR1 (photo 1) qui volait mieux que les avions alliés grâce à ses ailes épaisses, qui de surcroît ─étant plus rigides─ demandaient moins de haubans, ce qui diminuait encore la traînée. Manfred Von Richthofen dit "Le Baron Rouge", pilote le plus fameux de cet appareil était nommé ainsi car il peignait le sien en rouge pour attirer ses proies. Sa tactique efficace au début a toutefois montré un point faible puisqu’elle a finalement attiré un prédateur !

Photo 1 : Fokker DR I (photo Wikipédia)

Juste après la première guerre mondiale les progrès ont, comme on pouvait s’y attendre, stagné. Le DC3 de 1933 (photo 2) avec ses ailes "cantilever" représente la nouvelle révolution. Les ailes épaisses à forte inertie quadratique (section définissant la rigidité) permettent de se passer de haubans grands générateurs de traînée. Le fuselage de section circulaire minimise la surface projetée et donc la traînée. Les ailes effilées, le train rentrant, la cabine de pilotage fermée, l’absence de "verrues" sur le fuselage, les surfaces parfaitement lisses sont autant d’autres éléments qui ont enfin permis d’obtenir un avion fin au sens aérodynamique et donc rapide (plus de 300 km/h). L’essentiel de ce qui nous intéresse en aérodynamique est alors connu, mesuré et vérifié. Les progrès futurs viendront principalement des progrès de la propulsion.

Photo 2 : Douglas DC3 (photo Wikipédia)

A cette époque le NACA (ancêtre de la NASA) a enfin défini la première série systématique optimisée de profils d’aile. Ils sont désignés par quatre chiffres (NACA0009, NACA2412…). Ces profils sont idéaux pour nos modèles car ils sont optimisés pour le domaine aérodynamique qui nous concerne.

La seconde guerre mondiale apporte les profils laminaires plus efficaces aux hautes vitesses qui ne nous concernent pas. L’après guerre ajoute la touche finale (en dehors du domaine supersonique) avec les profils supercritiques pour le vol transsonique (utiles à certaines hélices) et la découverte que pour un fuselage, la surface mouillée compte plus que la section maîtresse. Il en résulte pour les avions de ligne les fuselages larges (un fuselage large mais court traîne moins qu’un fuselage étroit mais long car il a moins de surface mouillée pour une capacité donnée) et les fuselages affinés à l’arrière que l’on trouve sur les planeurs modernes en composite. C’est aussi durant cette période qu’apparaissent les "winglets" et autres surfaces secondaires. On notera à l’attention des maquettistes que les avions de combat à réaction modernes utilisent assez souvent un concept supplémentaire : le fuselage intégré aux ailes (photo 3). Il fait alors partie des surfaces portantes. La traînée qu’il engendre est alors utile car elle contribue à la portance. Il faut alors tenir compte du fuselage pour calculer la portance.

Photo 3 : Lockheed Martin F22 (photo Wikipédia)

Notions de base

Traînée et portance

La relation physique 1 relative à la figure 1 définit la traînée Fx d’un corps plongé dans un fluide en mouvement à la vitesse Vt.

(1)

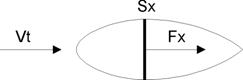
Figure 1 : traînée d’un corps dans un flux d’air

Dans cette expérience, peu importe que ce soit le fluide ou le corps qui soit en mouvement, ce qui compte c’est qu’il y ait une vitesse relative Vt entre les deux. La traînée générée par le fluide (l’air dans notre cas) est une force Fx proportionnelle au carré de la vitesse Vt, à la masse volumique r du fluide, à la section maîtresse Sx du fluide (surface maximale de la coupe du corps prise perpendiculairement au vecteur de vitesse Vt, aussi appelée maître couple) et à un facteur de forme nommé Cx (aussi nommé traînée réduite). Le vecteur de force Fx a dans cette expérience la même orientation que le vecteur de vitesse Vt.

· Fx s’exprime en Newton : N (1 kg = 9,81 N)

· Vt s’exprime en mètre par seconde : m/s (1 m/s = 3,6 km/h)

· r s’exprime en kilogramme par mètre cube : kg/m³

· Sx s’exprime en mètres carrés : m²

· Cx appelé coefficient de traînée ou traînée réduite est une grandeur sans dimension

N. B. : au Japon, USA et quelques autres pays on utilise parfois les unités impériales (miles, livres, pieds…) pour cette formule. On ne peut dans ce cas l’appliquer qu’avec un coefficient de correction.

La masse volumique r de l’air est fonction de plusieurs paramètres (voir chapitre aérologie), mais dans les conditions normales à faible altitude on peut retenir la valeur de 1,2 kg/m³. Le coefficient Cx dépend évidemment de la forme du corps considéré, on peut retenir la valeur d’environ 1,2 pour une plaque plane carrée placée dans un plan perpendiculaire à l’écoulement, de 0,6 pour une sphère et 0,05 pour un corps fuselé (dans les meilleures conditions). Malheureusement, ces valeurs varient avec la dimension du corps et la vitesse du fluide, ce qui a créé de nombreux problèmes avant qu’on s’en rende compte.

Exemple : une balle de golf de 4 cm de diamètre lancée à 200km/h subira une force de traînée calculée ci-après :

Fx = (1,2/2)x0,6x(3,1416x0,02²)x(200/3,6)² = 1,39 Newton soit : 0,141 kg

La formule 1 est la formule de base de toute l’aérodynamique, mais la formule 2 ci-après relative à la figure 2, très proche, est encore plus importante. C’est la principale qu’utilisaient les pionniers. Elle donne la portance Fz d’une plaque plongée dans un fluide en mouvement à une vitesse Vt. La plaque représente naturellement une aile de surface Sa inclinée d’un angle a face au flux (incidence). Par définition, la portance Fz se situe dans un plan perpendiculaire au vecteur Vt. Dans la figure 2 la portance Fz est verticale vers le haut car la plaque est cabrée (inclinée vers le haut par rapport à la direction du flux).

(2)

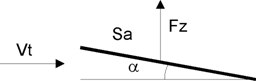
Figure 2 : portance d’une plaque plane dans un flux d’air

La formule 2 dit qu’une plaque (aile) placée à une incidence α dans un fluide de masse volumique ρ à vitesse Vt subit une force de portance Fz perpendiculaire au flux, proportionnelle à la surface de la plaque Sa, à la pente de portance a, à l’angle d’incidence α et au carré de la vitesse du fluide Vt.

· Fz s’exprime en Newton : N (1 kg = 9,81 N)

· Vt s’exprime en mètre par seconde : m/s (1m/s = 3,6 km/h)

· r s’exprime en kilogramme par mètre cube : kg/m³

· a est s’exprime degrés^-1(1/degré)

· a s’exprime en degrés

· Sa s’exprime en mètre carrés : m²

Le coefficient de pente a augmente avec l’allongement dans le plan perpendiculaire au flux de la plaque. Il est de l’ordre de 0,05 pour une plaque carrée, mais tend vers 0,11 pour une aile très allongée. L’angle a peut varier d’environ -10° à environ 10° (plus pour les ailes delta) ; au-delà le phénomène de décrochage fait disparaître la portance et la formule ne s’applique plus.

N. B. : on trouvera des formules anciennes utilisant sina au lieu de a. Le débat sur ce choix est resté ouvert jusqu’après la première guerre mondiale, car sur un angle limité à 10° il est difficile de distinguer les deux, étant donné les imprécisions des mesures.

Exemple : une plaque carrée de 20 cm de coté cabrée de 5° dans un vent de 60 km/h subira une portance calculée ci-après :

Fz = (1,2/2)x0,05x5x(0,2x0,2)x(60/3,6)² = 1,67 Newton soit : 0,17 kg

N. B. : le produit a.a nommé Cz est le coefficient de portance ou portance réduite. La valeur maximale de Cz (Cz max) pour une aile d’aéromodèle est d’environ 1,2, mais elle est plus élevée pour les avions grandeur avec une valeur typique de 1,6. Toutefois, elle peut atteindre 4 pour les ailes d’un avion de transport lorsque les volets d’hypersustentation sont sortis.

Effet d’échelle

Les deux formules précédentes ont posé de gros problèmes au début de l’aviation. On expérimentait sur des maquettes pour trouver Cx et Cz puis on extrapolait à l’avion grandeur…et ça marchait mal !

On s’est finalement rendu compte qu’en raison de la viscosité de l’air on ne pouvait changer la taille des objets étudiés sans modifier l’écoulement qu’à condition d’augmenter la vitesse ou la densité de l’air en proportion de la diminution d’échelle. En toute rigueur, deux écoulements ne sont similaires que s’ils présentent le même nombre de Reynolds Re défini par l’équation 3 :

Re = r.L.Vt/m (3)

Dans cette équation r représente la masse volumique du fluide, L une longueur de référence (typiquement la corde du profil d’aile étudié), Vt la vitesse du fluide et m sa viscosité dynamique. Dans le cas de l’air à pression et température normale (15°C et 1013 mbar) on peut utiliser la formule simplifiée 4 :

Re ≈ 70 000.L.Vt (4)

Dans l’équation 4 la longueur de référence L est exprimée en mètres et Vt la vitesse du flux d’air en m/s.

Exemple : un profil d’aile de 15 cm de corde dans un écoulement à 20 m/s verra un nombre de Reynolds Re de :

Re = 70000x0,15x20 = 210 000 : valeur courante dans l’univers aéromodéliste

On peut distinguer principalement trois domaines de nombre de Reynolds en aéromodélisme :

Très faibles Reynolds (< 100 000) :

C’est le domaine de l’indoor et des slowfliers. Dans cette zone des bulles d’air peuvent se former et se coller sur l’extrados des ailes. On est alors dans le domaine dit subcritique (qui est développé dans le paragraphe sur l’aérodynamique des faibles vitesses). Dans ce cas, les profils minces, style 1914 sont les meilleurs. Pour améliorer les résultats on peut être amené à ajouter des excroissances sur les ailes appelées turbulateurs destinées à empêcher les bulles qui se forment de se fixer en induisant un écoulement turbulent mais adhérent avant le point de formation naturel de ces bulles parasites.

Faibles Reynolds (de 100 000 à 1 000 000) :

C’est le domaine du modélisme classique. Dans cette zone les caractéristiques des profils changent beaucoup avec le nombre de Reynolds. Les profils d’ailes NACA à quatre chiffres, Clark, Eppler, Selig, etc. sont faits pour ce domaine. Le NACA n’a pas optimisé dans les années 1920 des profils pour l’aéromodélisme consciemment ; il l’a fait parce qu’il n’avait pas encore pleinement conscience du problème de l’effet d’échelle, et que ses souffleries soufflant typiquement à 20 m/s recevaient par chance pour nous des profils d’environ 15 cm de corde !

Reynolds au dessus d’un million :

C’est le domaine de l’aviation grandeur. Le nombre de Reynolds influe moins sur la polaire dans cette zone et les Cz max sont bien plus élevés. Par contre, la zone d’écoulement adhérent turbulent gâte de plus en plus le profil (voir paragraphe sur les traînées), ce qui a conduit au développement de profils particuliers dits laminaires mis au point à l’orée de la seconde guerre mondiale (profils NACA à 6 chiffres commençant par 6). Ils sont moins bons que les profils NACA à 4 chiffres dans le domaine des faibles Reynolds. Certains fabricants d’aéromodèles les utilisent malgré tout, sans doute par méconnaissance. Les avions de transport grandeur n’utilisent plus depuis longtemps ces profils NACA à 6 chiffres, car ils sont confrontés au problème de compressibilité qui justifie l’usage de profils relativement minces moins galbés sur l’extrados, dits supercritiques. Ces derniers nous sont utiles pour les hélices de racers et autres hélices rapides (voir paragraphe sur l’aérodynamique des hautes vitesses).

Idées fausses

La formule 1 suggère que plus le maître couple est faible plus la traînée est faible ; c’est pourquoi il faut choisir un fuselage aussi effilé que possible et une aile aussi mince que possible. D’où les profils minces du début de l’aviation et les énormes fuselages de certains chasseurs de la seconde guerre mondiale qui prolongeaient le maître couple du moteur en s’amincissant le plus progressivement possible.

En fait, la traînée d’un corps profilé est d’abord fonction de sa surface mouillée. Pour un volume donné, on obtient la plus faible surface mouillée avec une sphère, qui n’est hélas pas un corps profilé. Dans le domaine de Reynolds du modélisme classique, la forme proche de l’idéal est un corps de section circulaire d’une longueur environ trois à quatre fois supérieure au diamètre et ressemblant à celui de la figure 1 (cf. les fuselages des planeurs modernes). Dans le cas des ailes, augmenter l’épaisseur n’augmente que peu la surface, donc la traînée. Par contre, elle augmente significativement la portance maximale et la solidité mécanique. On a donc à tort oublié dans le monde de l’aéromodélisme les profils épais à 15 % et 18 % d’épaisseur relative largement utilisés dans le monde modéliste des années 60.

Une autre idée fausse consiste à croire que la forme idéale est la forme de la goutte d’eau. En fait, les gouttes d’eau n’ont pas la forme que l’on croit en général. Lorsqu’elles sont très petites elles sont sphériques à cause de la tension de surface. Lorsqu’elles grossissent, elles prennent la forme d’une sphère aplatie à l’avant pas du tout aérodynamique. Si elles grossissent encore, la pression due à la vitesse les fait éclater (c’est pour cette raison qu’on ne prend jamais sur la tête des gouttes d’un litre…). La forme idéale, pour nos nombres de Reynolds, est celle de la figure 1 qui n’est pas du tout celle d’une vraie goutte d’eau. Elle a été définie dans les souffleries des années 20, époque où les souffleries travaillaient avec les nombres de Reynolds de notre hobby.

Les traînées

Notion de traînée et classement

La traînée, force qui s’oppose à la vitesse et gène l’avancement est une préoccupation centrale des aérodynamiciens. De sa diminution dépend l’efficacité des avions de transport. Avant 1930 on était incapables de la maitriser, on ne disposait tout simplement pas des connaissances requises. En modélisme ce n’est une préoccupation centrale que pour les planeurs et racers car les autres aéromodèles ne cessent de monter et descendre et les moteurs servent plus à vaincre la gravité que la traînée. Malgré tout, il est important de bien comprendre la nature, les causes et les effets de la traînée, même si on ne cherche pas à la minimiser, car une gestion efficace de la traînée a de nombreux effets secondaires sur la stabilité de vol, le comportement en décrochage, etc..

On peut classer les traînées en quatre sortes d’origine différente, qui n’ont ni les mêmes ampleurs, ni les mêmes conséquences.

· La traînée de forme liée à la forme de l’objet aérodynamique

· La traînée induite provoquée par la portance des ailes

· La traînée de friction induite par la friction de l’air sur les surfaces

· La traînée d’onde générée à haute vitesse par une onde de choc

Traînée de forme

La traînée de forme est la plus importante et de loin lorsqu’elle n’est pas éliminée ; c’est celle des écoulements décollés.

Lorsqu’un corps n’est pas profilé, l’écoulement n’arrive plus à suivre sa surface, il se décolle. On parle alors d’écoulement décollé turbulent. Le problème principal est que cet écoulement n’est pas stable, il change en permanence de direction et de vitesse, d’où le terme "turbulent". C’est en fait un mouvement oscillatoire entretenu du flux d’air en aval de l’obstacle. Ce mouvement d’air de forte amplitude consomme beaucoup d’énergie et génère donc beaucoup de traînée.

Cette traînée peut s’évaluer à l’aide de l’équation 1 en prenant Cx ≈ 1. Le Cx peut dans certains cas dépasser 1 et atteint même environ 1,3 pour les parachutes de type hémisphérique. L’écoulement autour d’un câble cylindrique est un peu moins pénalisant, le Cx étant dans ce cas aux environs de 0,6. Dès qu’un corps est suffisamment profilé ─courbes progressives, pas de protubérances, d’ondulation, de rugosité excessive, etc.─ l’écoulement devient adhérent et ce Cx tombe en dessous de 0,01 à nos Reynolds..

Juste avant la seconde guerre mondiale, l’optimisation aérodynamique d’un avion de chasse aux US consistait principalement à mettre la cellule à optimiser dans une soufflerie après avoir parfaitement lissé la surface et éliminé tous les accessoires. On mesurait ensuite l’évolution de la traînée après l’ajout de chaque accessoire en essayant de modifier ou éliminer les accessoires trop pénalisants. Après cet exercice, le fuselage présentait une traînée comprise entre 1,5 et deux fois celle du fuselage parfaitement propre. Aérocalc prend en compte ce terme de "propreté".

Il est essentiel de comprendre qu’un écoulement peut évoluer de deux façons radicalement opposées :

· soit il est stable, dit laminaire, et engendre peu de traînée,

· soit il est instable, dit turbulent, et engendre beaucoup de traînée.

Si un flux d’air rencontre une perturbation (obstacle, autre flux d’air, etc.) il y a deux possibilités, soit le flux se déplace localement puis reprend son chemin normalement sans générer de traînée importante, soit une oscillation du flux d’air s’amplifiant de façon catastrophique s’amorce générant des mouvements importants et une très forte traînée.

Si un obstacle non profilé génère toujours l’oscillation si pénalisante, elle peut aussi être induite par une surface profilée là ou on ne l’attend pas : jonction de fuselage avec d’autres éléments, section de fuselage à bord vif, etc.. Dans ce cas il faut être capable d’identifier le phénomène (pas facile sans soufflerie) et de trouver le petit élément aérodynamique adapté capable de l’éliminer en stabilisant l’écoulement. Entre les ailes et le fuselage on est souvent obligé d’ajouter un raccord arrondi appelé raccord Karman du nom de l’inventeur. Des ailerons ou autres surfaces aérodynamiques fixes bien placés dans le sens de l’écoulement sont souvent ajoutés sur les fuselages d’avions grandeur modernes et permettent de supprimer les velléités de l’écoulement à devenir instable.

A titre d’anecdote, le Lockheed P38 Lightning [3] (photo 4), célèbre avion de chasse de la seconde guerre mondiale à deux queues (le dernier avion de Saint Exupéry) a vu le Cz maximum (portance maximale) de ses ailes augmenter de 30 % et donc la vitesse d’atterrissage diminuer de 15 % du fait de l’ajout de raccords Karman, en même temps que la précision de pilotage augmentait considérablement.

Photo 4 : raccords Karman ajoutés au P-38

(Pilote Dick Bong, photo Wikipédia)

Traînée induite

La traînée induite, dominante lorsque Cz est élevé, est la traînée induite par la portance (valeur réduite Cxi). En effet, la portance génère des tourbillons marginaux inévitables à l’extrémité des ailes, d’où une traînée. Le calcul et la diminution de cette traînée est expliquée plus loin dans ce chapitre. Disons simplement ici que pour la diminuer il faut augmenter l’allongement des ailes (d’où l’allongement parfois démesuré des ailes de planeur) et les effiler, c'est-à-dire diminuer leur corde au fur et à mesure qu’on s’approche du saumon.

Comme on n’avait pas encore cette notion durant la première guerre mondiale, les ailes des avions des pionniers et de la "grande guerre" étaient presque invariablement rectangulaires avec parfois un très faible allongement comme sur la "Demoiselle" de Santos Dumont [4] (photo 5), premier avion construit en série dont les caractéristiques étaient fortement dégradées par la traînée induite excessive.

Photo 5 : Aéroplane "Demoiselle" (photo Wikipédia)

Noter le très faible allongement des ailes de forme rectangulaire

Traînée de friction : couche limite

Si les fluides n’étaient pas visqueux, il n’y aurait plus de traînée dès qu’il n’y a plus de décollement et de tourbillon marginal dû à la portance, quelle que soit la forme considérée. Malheureusement, la viscosité de l’air provoque le freinage du fluide à proximité immédiate de la surface léchée. Cette couche de quelques millimètres d’épaisseur sur nos modèles et de quelques centimètres sur les avions grandeur s’appelle couche limite et est le siège de dissipation d’énergie par ralentissement du flux d’air, et donc de traînée. On appelle cette traînée irréductible la traînée de friction.

Cette traînée inévitable apparait sur toutes les surfaces (ailes, fuselage, empennage…) longées par un fluide. Elle est proportionnelle à cette surface nommée surface mouillée par analogie avec les coques de bateaux sur lesquelles on a en premier identifié cette traînée.

Il faut distinguer sur toute surface deux cas différents séparés géographiquement par un point de transition :

Ecoulement laminaire :

C’est un écoulement parfaitement stable et continu. On le trouve toujours à l’avant des ailes et du fuselage. Il est marqué par un coefficient de traînée faible qui diminue très rapidement avec le nombre de Reynolds (voir figure 4).

Point de transition :

En amont de l’écoulement le flux est laminaire, à moins d’avoir des défauts aux bords d’attaque des ailes ou à l’avant du fuselage. Mais on passe invariablement à un écoulement turbulent avant la fin de la surface. On appelle le point de passage de l’écoulement laminaire à turbulent le "point de transition". Le point de transition se situe typiquement à l’endroit où la section commence à diminuer. On joue sur la forme des profils d’aile et de fuselage pour faire reculer ce point, car plus on le recule plus la traînée de friction globale diminue. Malheureusement, le gain n’est pas énorme, surtout pour les faibles nombres de Reynolds.

Ecoulement turbulent :

C’est un écoulement adhérent grâce à l’effet Coanda, [5] fait de micro-turbulences. Il apparaît toujours en aval de l’écoulement laminaire à partir du point de transition sur les ailes et le fuselage. Cet écoulement a un coefficient de traînée supérieur au précédant à cause de l’énergie perdue dans les micro-turbulences. Ces turbulences engendrent un coefficient de traînée supérieur à celui de l’écoulement laminaire (voir figure 4). De plus, cette traînée diminue moins vite avec l’augmentation du nombre de Reynolds.

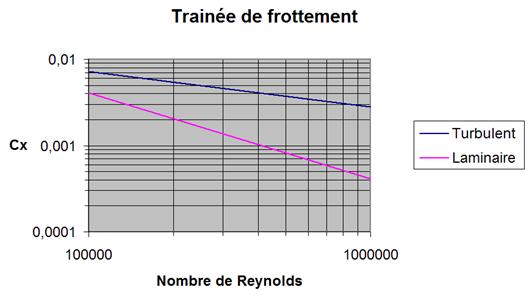
Figure 4 : évolution de la traînée de frottement laminaire et turbulente en fonction du nombre de Reynolds

La figure 4 donne l’évolution des Cx des deux écoulements en fonction du nombre de Reynolds. Cette figure amène deux remarques :

1. Les frictions diminuent lorsque l’échelle augmente. L’aviation grandeur souffre donc relativement moins de la viscosité que nous. A contrario tout se passe pour les insectes comme s’ils évoluaient dans un air gluant. Les grands avions ont donc une plus grande finesse. A titre d’exemple, la finesse d’un A380 est de 21 alors que celle d’un aéromodèle fin atteint tout juste 10.

2. Plus le nombre de Reynolds augmente, plus l’écart entre traînée laminaire et turbulente s’accroît. C’est entre autre ce dernier point qui fait que les profils utilisés ne sont pas les mêmes en modélisme et aviation de loisir grandeur. Comme on a intérêt à optimiser Cx min/Cz max, en modélisme on cherchera plutôt à maximiser Cz max, limité pour les faibles Reynolds (profils NACA à 4 chiffres), alors qu’en aviation de tourisme on cherchera plutôt à minimiser Cx min en utilisant des profils laminaires (profils NACA à 6 chiffres commençant par six) qui reculent le point de transition et donc la traînée, ce qui avec les nombres de Reynolds supérieurs à un million fait mieux que compenser le Cz max diminué.

Traînée d’onde

Le dernier type de traînée est la traînée d’onde. Il s’agit de l’onde de choc supersonique apparaissant lorsque la vitesse du flux d’air accéléré par une surface dépasse localement celle du son. En ce qui nous concerne, ça n’arrive que sur les hélices de racers et dans le cas d’utilisation de moteurs tournant à des régimes excessifs.

Les avions de transport qui volent typiquement dans le domaine transsonique à Mach 0,85 (85 % de la vitesse du son) utilisent des profils d’aile adaptés dits supercritiques (épaisseur relative faible et galbe diminué sur l’extrados) qui limitent la traînée d’onde dans le domaine transsonique. Ils sont aussi à utiliser pour les hélices rapides (compétition).

Ca ne nous concerne pas en modélisme, mais il est néanmoins intéressant de savoir qu’en vol supersonique c’est la traînée d’onde qui limite la performance des avions et fait chauffer l’air à haute température au voisinage de la cellule. A titre indicatif, à Mach 2, la moitié de la traînée était due à l’onde de choc sur Concorde qui n’avait alors qu’une finesse de 6 à comparer à la finesse de 18 du Boeing 747 de la même époque qui consomme la même quantité de kérosène en transportant cinq fois plus de passagers… Contrairement à ce qu’on pourrait croire, voler moins vite n’aurait rien résolu car la traînée d’onde diminue ─contre toute attente─ avec lorsque la vitesse augmente. Ce qui limitait la vitesse de vol de Concorde était la chaleur ; l’alliage d’aluminium de Concorde ne supportait pas plus que la chaleur engendrée par Mach 2,05. L’avion était bridé par le mur de la chaleur.

Caractéristiques des profils d’aile

Concepts

L’étude des ailes des aéronefs est complexe car l’écoulement est en trois dimensions. Pour cette raison on étudie toujours dans un premier temps les profils, les ailes étant étudiées dans leur globalité dans un second temps. Un profil est une section d’aile dans la direction de l’écoulement du fluide choisie à un endroit donné de l’aile (les ailes ont souvent un profil constant en modélisme, mais rarement en aviation grandeur). L’étude se fait en créant matériellement ou virtuellement une aile d’envergure infinie dont la section est celle du profil à étudier. L’écoulement se fait alors en deux dimensions dans le plan du profil, ce qui simplifie considérablement l’étude.

Un profil dans un flux d’air en mouvement génère trois réactions fondamentales : la traînée, la portance, et le couple de basculement. Pour des raisons de commodité on étudie ces valeurs sous forme dite réduite :

· traînée réduite Cx telle que dans la formule 1, en remplaçant toutefois le maître couple Sx par la surface portante Sa pour des raisons d’homogénéité avec les deux formules suivantes,

· portance réduite Cz qui correspond au produit a.α de la formule 2,

· couple de basculement réduit Cmo pris à 25 % de la corde en partant de l’avant (foyer), défini par la formule 5 ci-après.

(5)

On remarquera que la formule 5 est similaire aux deux précédentes. Seule la corde c a été ajoutée pour des questions d’homogénéité physique car on mesure ici un moment (produit d’une force par une longueur) et non une force pure.

Les questions qui viennent immédiatement à l’esprit sont : qu’es ce que c’est que ce couple et pourquoi à 25% ?

En fait, on c’est rapidement aperçu dans les premières expériences que selon l’endroit où on maintenait le profil dans la soufflerie, il présentait une tendance à basculer en avant ou en arrière. Pour une plaque plane, la tendance à basculer disparaissait si elle était maintenue précisément à 25 % de la corde en partant de l’avant, d’où le choix de définir de moment de basculement à 25 % de la corde. On appelle cette position : foyer. Donc pour une plaque plane maintenue au foyer on a Cmo = 0. Pour un profil quelconque, on a constaté une autre propriété remarquable du foyer : Cmo reste à peu près constant quelle que soit l’incidence du profil dans le flux d’air si on mesure le couple à cet endroit précis. En raison de cette dernière propriété le foyer est un point fondamental (point de référence) pour l’étude de la stabilité abordée dans un prochain chapitre.

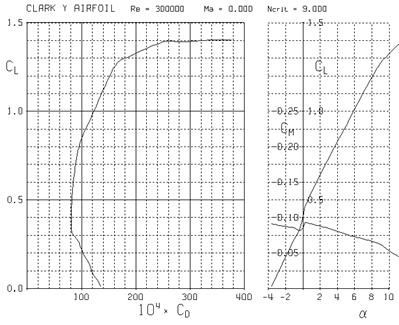
La figure 5 montre le profil très répandu Clark Y, sa polaire et ses grandeurs principales.

N. B. : les courbes ci-après (comme la majorité des copies d’écran de cet ouvrage) utilisent les notations anglo-saxonnes très largement utilisées hors de France. Les anglo-saxons utilisent Cl (l pour lift = portance) à la place de Cz et Cd (d pour drag = traînée) à la place de Cx.

Figure 5 : profil Clark Y et sa polaire obtenus avec la soufflerie numérique Xfoil

Ce profil dessiné pour la RAAF dans les années 1920 peut être considéré comme idéal pour nos modèles courants, pour peu qu’ils n’aient pas à faire d’acrobatie avec accélération négative (vol sur le dos).

La partie haute de la figure 5 donne le profil, facile à réaliser grâce à l’intrados plat sur une grande partie de la corde. La courbe en bas à droite donne la portance et Cmo en fonction de l’incidence. Elle peut se résumer à trois valeurs à peu près constantes :

· a : la pente de portance ≈ 0,11,

· αo : l’incidence à portance nulle = -3,65° qui indique qu’il faut incliner un peu le profil vers le bas pour qu’il cesse de porter,

· Cmo = -0,0812 qui indique que le profil a tendance à basculer vers l’avant (moment piqueur).

En bas à gauche, la courbe donne la traînée réduite Cx en fonction de la portance réduite Cz. Cette courbe a été baptisée « polaire » par Eiffel mais a été utilisée en premier par Lilienthal aux environs de 1880. Elle donne les caractéristiques principales d’un profil, puisqu’à une vitesse donnée on connaît Cz car le poids est juste compensé par la portance et que le Cx déduit de la polaire donne la traînée. La finesse et le taux de chute sans moteur sont finalement déduits de la portance et la traînée.

Comme la polaire est la caractéristique fondamentale d’un profil, on a cherché dès les prémices de l’aviation à obtenir le profil aux meilleures polaires.

Figure 6 : traînées des profils plats, minces galbés et épais

Les pionniers, en vertu de la formule 1 ont à tort d’emblé éliminé les profils épais, mais se sont aperçu qu’en galbant la plaque faisant office d’aile, le Cz maximum augmentait du coté des incidences positives et diminuait du coté des incidences négatives (effet également visible sur le profil Clark Y). Ceci permettait de diminuer la surface et par voie de conséquence le poids et la traînée Fx (voir centre de la figure 6). Le galbe est défini par la courbure relative en % correspondant à l’écart relatif maximum du profil par rapport à une droite reliant le bord d’attaque au bord de fuite (c'est-à-dire cent fois l’écart maximum divisé par la corde).

Tous les profils de 1890 à 1917 ont été du type plaque mince galbée ; les vertus de la plaque plane n’ayant été découvertes que très récemment dans les salles sport…C’est à ce moment qu’à Göttingen on a découvert que les profils épais permettaient d’augmenter encore Cz sans augmenter significativement Cx. Ainsi, on pouvait diminuer la surface des ailes une nouvelle fois et diminuer encore la traînée (voir bas de la figure 6). Cette découverte allemande a donné durant un temps un avantage à l’Allemagne et ses alliés.

Aujourd’hui on n’utilise plus que des profils épais (typiquement de 8 % à 18 % d’épaisseur relative) plus ou moins galbés en fonction de la plage de vitesse désirée, et avec une position de l’épaisseur maximale plus ou moins reculée en fonction du nombre de Reynolds. L’ajustement fin de la forme de l’extrados et de l’intrados permettent d’optimiser au-delà des trois premiers critères chaque profil en fonction de l’usage exact auquel il est destiné. Cette optimisation se faisait dans des souffleries dans les temps anciens, et ce fait aujourd’hui à l’aide de logiciels appelés souffleries numériques. Quoi qu’il en soit, peu de modélistes créent encore des profils car on dispose aujourd’hui d’un catalogue pléthorique en mesure de satisfaire quasiment tous les besoins. On peut récupérer dans l’archive profils2.zip un extrait de ces profils (choix de 1552 profils courants…). Les seuls cas où la conception d’un profil a encore un sens est la compétition. Et encore ! En racer les meilleurs profils sont bien déterminés et en planeur ils dépendent de l’aérologie précise du moment, aérologie toujours imprévisible…

Les profils les plus courants

Comme on vient de le voir, des myriades de profils sont disponibles, mais il faut savoir plusieurs choses :

· Une grande majorité sont faits pour des nombres de Reynolds autres que les nôtres et perdent toutes leurs propriétés dans notre domaine, comme le merveilleux NACA 23012 du P38 de Lockheed ─dessiné par Kelly Johnson─ avec lequel St Exupéry nous a quitté.

· Une énorme quantité n’a été développée qu’à des fins d’études scientifiques et n’a pas de caractéristiques intéressantes en ce qui nous concerne.

· Dans la majorité des cas (acrobatie et modélisme loisir) le Cx a peu d’importance car le moteur est surpuissant (déterminé par rapport à la capacité ascensionnelle), ce qui permet de se contenter des profils les plus ordinaires avec un bon Cz max sans autre état d’âme.

· Le facteur principal fixant le Cx d’un profil n’est pas sa forme, mais son état de surface qui peut faire varier la traînée d’un facteur de deux ou plus (cf. Javafoil [8] de Martin Hepperle).

· Le facteur suivant n’est pas non plus la forme, mais la régularité de variation de courbure. Le moindre creux, la moindre bosse fausse tout…

· Tout élément parasite accroché à la surface provoque des turbulences et ruine le profil. Autrement dit, si vous avez une chape ou un guignol non totalement caréné qui dépasse quelque part, inutile de chercher le profil idéal. Il y a plus à gagner à caréner ou enlever ce qui dépasse, même les surépaisseurs d’entoilage…

· Enfin, si votre aéromodèle n’a pas un fuselage de taille réduite au maximum, parfaitement profilé et sans protubérance, c’est lui qui limitera le Cx plutôt que le profil.

L’expérience a montré qu’il est extrêmement difficile d’obtenir des résultats reproductibles en soufflerie à cause des imperfections de surface inévitables des modèles. De plus les résultats dépendent fortement des caractéristiques de chaque soufflerie à cause, entre autres, du bruit et des vibrations propres qu’elles génèrent. Deux polaires ne peuvent donc être comparées que si les profils utilisés sont parfaits et que si elles ont été obtenues par le même moyen et dans strictement les mêmes conditions. Ceci se résume simplement pour nous : on ne peut comparer que des polaires obtenues par un même logiciel de soufflerie numérique. Les souffleries numériques libres écrites pour les faibles Reynolds sont Xfoil [7] de Mark Drela, et Javafoil [8] de Martin Hepperle (moins précise mais beaucoup plus conviviale).

Les onze profils présentés ci-après sont représentatifs des besoins des divers domaines de l’aéromodélisme. Ils suffisent pour tous les cas courants, excepté pour les compétiteurs de racer et planeur qui doivent gagner des dixièmes de seconde ou de points de finesse ; ils piocheront dans le restant de la myriade de centaines de profils, ou en ajouteront un portant leur propre nom. Pour chacun des profils présentés le Cz max au nombre de Reynolds 200 000 et le Cx min au nombre de Reynolds 400 000 sont indiqués, tandis que le profil et la polaire provenant de JavaFoil (sauf exception) sont montrés et accompagnés d’un bref commentaire.

N. B. : on peut obtenir la finesse maximale d’un profil pour un nombre de Reynolds donné en traçant la tangente au profil partant de l’origine. La finesse est Czo/Cxo, Czo et Cxo étant la portance et traînée réduite au point de contact de la tangente avec la courbe. Par exemple, pour le profil Clark Y à 200 000 Reynolds la tangente touche à Czo = 1,1 et Cxo = 0,016, ce qui donne une finesse maximale de 69. Un modèle ordinaire ayant une finesse de l’ordre de 10 on peut immédiatement en déduire que les sources de traînées principales ne viennent pas du profil.

Clark Y : profil à 11,7 % d’épaisseur relative maximale et environ 4 % de courbure relative par rapport à la ligne moyenne. Il est fait pour tous les cas courants et est facile à mettre en œuvre car il est plat sur la majeure partie de l’intrados. Si vous n’avez pas d’exigence spéciale et ne souhaitez pas faire d’acrobatie, c’est ce profil qu’il vous faut. Il couvre la majorité des besoins (noter les différences de polaire entre Xfoil figure 5 et JavaFoil figure 8).

Cz max 1,3 Cx min 0,007 à Cz 0,4

Figure 7 : profil Clark Y, profil universel à intrados plat sauf à l’avant

Figure 8 : polaire du profil Clark Y

Naca 2412 : variante du profil précédant. La courbure est diminuée à 2 % pour conserver une portance suffisante en vol dos. Il est pour ceux qui veulent pouvoir faire un peu d’acrobatie avec accélération négative (vol inversé). Comme aucune des faces n’est plane, la réalisation d’ailes avec ce profil est plus compliquée qu’avec un profil Clark Y.

Cz max 1,1 Cx min 0,007 à Cz 0,2

Figure 9 : profil Naca 2412, profil universel permettant le vol inversé

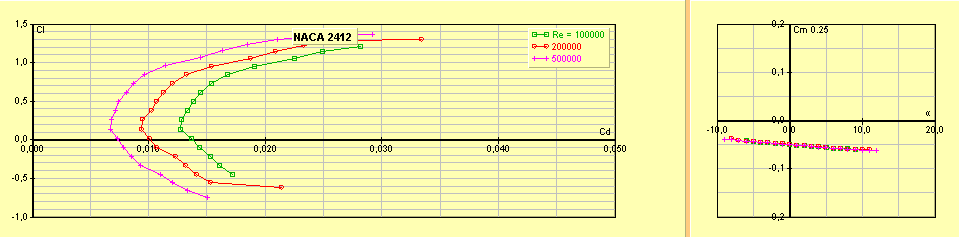
Figure 10 : polaire du profil Naca 2412

Eppler 475 : profil symétrique pour les acrobates. L’épaisseur relative maximale de 15 % très en avant permet de préserver un bon Cz max malgré l’absence de cambrure du profil. Comme il est symétrique il se comporte de la même façon sur le dos et sur le ventre, ce qui est un avantage évident en acrobatie. Bien que ce profil soit excellent, de nombreux avions d’acrobatie d’aujourd’hui se contentent d’un profil d’épaisseur relative de 12 % nettement moins porteur. La raison de cette évolution est inconnue et curieuse. Il s’agit peut être d’une perte de connaissance ?

Cz max 1,2 Cx min 0,01 à Cz 0

Figure 11 : profil Eppler 475, profil symétrique pour l’acrobatie

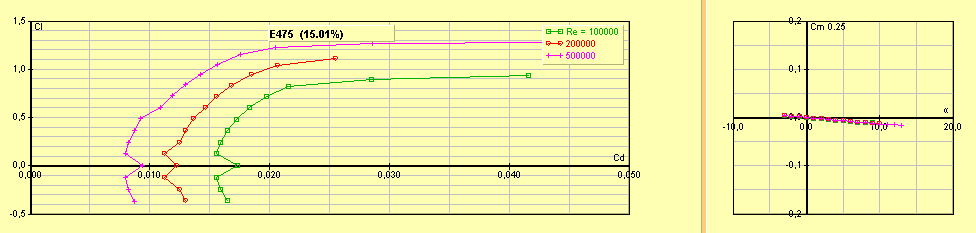
Figure 12 : polaire du profil Eppler 475

Fauvel : profil autostable (Cmo positif qui donne un couple braqueur) à 14 % d’épaisseur relative maximale et à cambrure reflex (courbure inversée du coté du bord de fuite). Il est conçu pour les ailes volantes car grâce à son couple braqueur il peut se passer d’empennage (voir chapitre sur la stabilité). Nous devons ce profil à l’ingénieur français Charles Fauvel [6] à qui l’on doit de nombreuses ailes volantes conçues et fabriquées de 1929 à 1971. Noter la partie arrière concave de l’extrados qui complique la construction.

Cz max 1,35 Cx min 0,009 à Cz 0

Figure 13 : profil Fauvel, profil autostable pour les ailes volantes

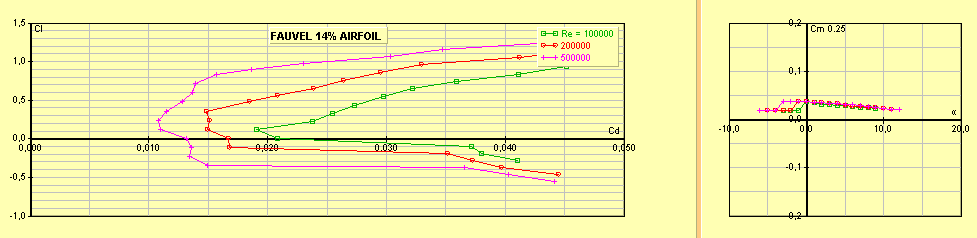
Figure 14 : polaire du profil Fauvel

MH43 : profil d’épaisseur maximale 8,5 %. Profil spécial pour racer dû à Martin Hepperle. Il est fait pour les très fortes plages de vitesse lorsque la charge alaire maximale est imposée par un règlement de compétition.

Cz max 0,95 Cx min 0,0062 à Cz 0,1

Figure 15 : profil MH43, profil pour racer

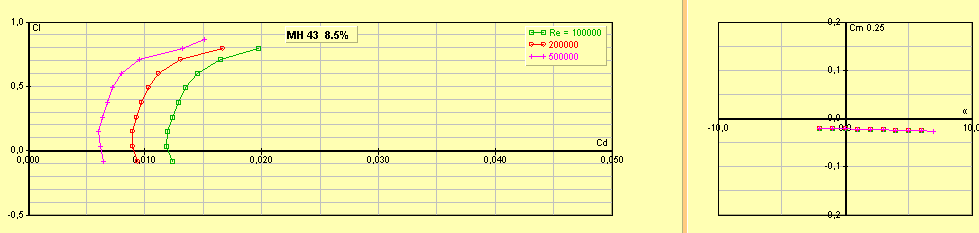
Figure 16 : polaire du profil MH43

B29 emplanture : profil « provocation », opposé du précédant, 22 % d’épaisseur relative maximale ! Il était comme son nom le suggère utilisé à l’emplanture des ailes des célèbres bombardiers américains qui ont entre autre brûlé et irradié le japon. Ce profil démontre à ceux qui ne veulent pas l’admettre qu’un fort maître couple ne nuit pas nécessairement aux performances. Sa forte épaisseur augmentant la résistance intrinsèque de l’aile permettait de construire plus léger, ce qui permettait de diminuer la surface alaire, ce qui diminuait finalement la traînée ; CQFD. Si en racer la règlementation imposait une vitesse de vol minimale plutôt qu’une charge alaire maximale, ce profil serait à peu près aussi bon que le précédant…

Cz max 1,3 Cx min 0,0105 à Cz 0,1

Figure 17 : profil B29 emplanture, profil de bombardier subsonique de la secondaire mondiale

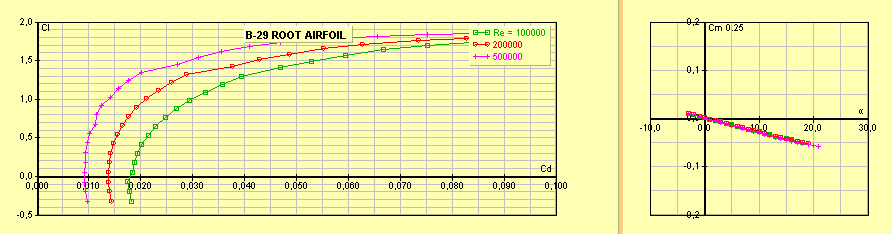
Figure 18 : polaire du profil B29 emplanture

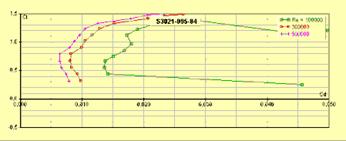
S3021 : profil à 9,5 % d’épaisseur relative maximale dû à Selig. Pour planeur de compétition qui privilégie un peu la gratte. Le Cx min est très bas, mais augmente rapidement lorsque Cz passe en dessous de 0,2 ; ce qui gêne la pénétration.

Cz max 1,2 Cx min 0,0068 à Cz 0,3

Figure 19 : profil S3021, profil pour planeur de compétition qui privilégie la gratte

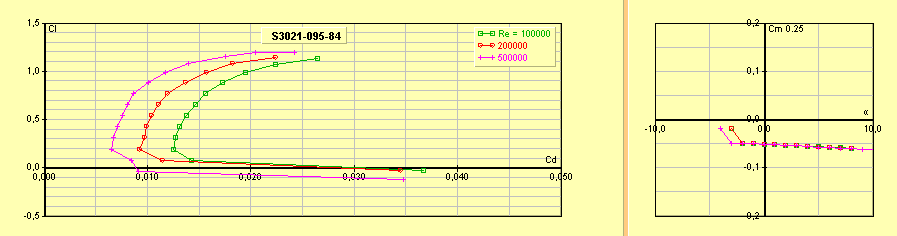
Figure 20 : polaire du profil S3021

S7012 : profil à 8,75 % d’épaisseur relative maximale aussi dû à Selig, pendant du précédant pour planeur de compétition qui privilégie plutôt la pénétration. Cz max est plus faible que pour le profil précédant, mais on peut voler à Cz égal à 0,1 sans augmenter la traînée d’où une meilleure pénétration. Noter la partie arrière concave de l’intrados qui complique la construction.

Cz max 1,05 Cx min 0,0062 à Cz 0,05

Figure 21 : profil S7012, profil pour planeur de compétition qui privilégie la pénétration

Figure 22 : polaire du profil S7012

SB96 12.7/3.0 : Profil pour planeur de loisir dû à Serge Barth. Comme son nom le suggère, il fait 12,7 % d’épaisseur relative maximale pour une courbure relative de 3 %. Il est remarquable par son Cz max très élevé et un très faible Cx à faible Cz. Donc il gratte et pénètre admirablement bien. De plus, son Cz et son épaisseur relative très élevés, autorisent une faible surface et donc une construction légère, ce qui est idéal pour les grandes plumes dont il faut limiter le poids au maximum afin que le lancer à la main reste raisonnablement possible. Noter la partie arrière concave de l’intrados qui complique la construction.

Cz max 1,45 Cx min 0,008 à Cz 0,2

Figure 23 : profil SB96 12.7/3.0, profil pour planeur de loisir à forte portance maximale

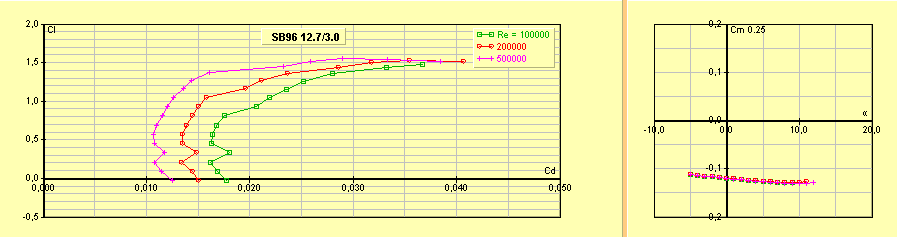
Figure 24 : polaire du profil SB96 12.7/3.0

Naca 0009 : profil symétrique profilé d’épaisseur relative 9 % pour les empennages. Utilisé lorsqu’on désire un empennage à faible traînée.

Cz max 0,7 Cx min 0,010 à Cz 0

Figure 25 : profil symétrique Naca 0009 pour les empennages

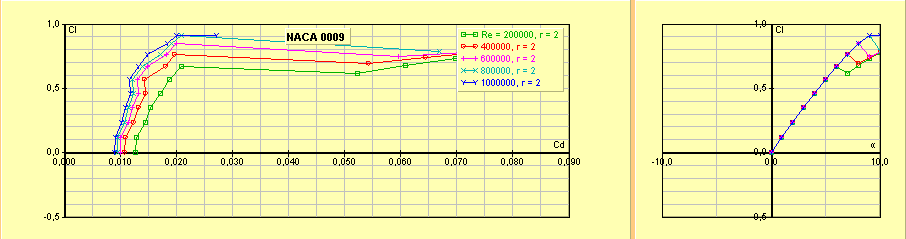
Figure 26 : polaire du profil Naca 0009

Plaque plane à 10 % : profil très utilisé pour les stabilisateurs et les dérives mais dont les propriétés sont ignorées de beaucoup.

Cz max 0,9 Cx min 0,011 à Cz 0,25

A condition que le bord d’attaque soit arrondi correctement et le bord de fuite effilé, c’est un profil acceptable (voir figure 27). Par contre, les figures 28 et 29 montrent parfaitement que si le bord d’attaque est mal arrondi, le profil peut devenir très mauvais suite à un décollement du flux d’air. Les polaires ont été établies dans le cas présent avec la soufflerie numérique commerciale VisuAéro. On notera que Visuaéro a tendance à être plus optimiste sur les Cz max que JavaFoil.

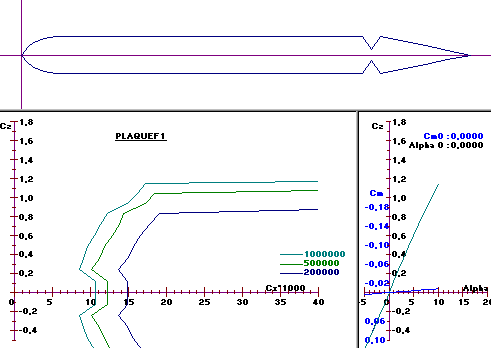
Figure 27 : plaque plane avec bord d’attaque correctement arrondi selon Visuaéro

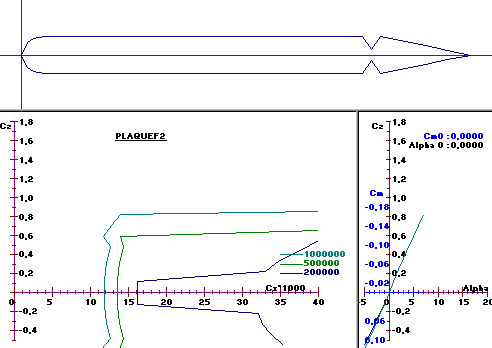
Figure 28 : plaque plane avec arrondi trop court selon Visuaéro

Figure 29 : plaque plane avec arrondi trop long selon Visuaéro

Choix d’un profil

La façon classique de choisir un profil est de le prendre parmi la dizaine qui viennent d’être présentés en fonction du type de modèle auquel on souhaite l’appliquer. Si on est très exigeant parce qu’on veut un modèle de hautes performances, on pourra sélectionner un autre profil parmi la palette des 1500 et quelques profils téléchargeables plus haut.

Cette seconde méthode, accessible à un aérodynamicien expérimenté, nécessite toutefois un temps dissuasif pour un amateur, car il faut charger chaque profil dans une soufflerie numérique, tracer les polaires et les comparer entre elles. L’aérodynamicien expérimenté n’est obligé de faire ce travail que pour quelques profils, et ce pour trois raisons :

· Il sait que les profils sont classés par familles d’application et connaît ces familles et applications ; il lui suffira donc de trier dans la famille qui correspond à son application.

· Il sait approximativement qu’elle épaisseur relative et quelle cambrure est adaptée à son besoin. Les règles assez sont simples : à nos Reynolds, plus un profil est épais, plus il est porteur, mais plus sa traînée est importante ; plus un profil est cambré, plus la traînée minimum apparaît à un Cz élevé. En fin de compte, plus on veut une plage de vitesse importante, moins on cambre le profil et plus on le choisit mince.

· Il dispose déjà de nombreuses polaires pré imprimées réalisées au fur et mesure de la conception d’aéromodèles.

Entrer dans le détail des familles de profils sort du cadre de cet ouvrage car il faudrait y consacrer un espace trop important par rapport à l’utilité pour l’aéromodéliste moyen. Si on est vraiment intéressé, on pourra consulter des ouvrages spécialisés et faire quelques essais avec une soufflerie numérique gratuite comme Xfoil [7] ou JavaFoil [8].

Les perfectionnistes utilisent parfois une troisième méthode. Elle consiste a partir d’un profil proche de celui recherché, de le charger dans une soufflerie numérique, puis de le modifier jusqu’à obtenir un profil parfaitement optimisé pour son application. Comme pour la seconde méthode, une bonne expérience est indispensable.

Souffleries numériques

Les souffleries servent à tester et optimiser les profils (souffleries 2D) ou les avions entiers (souffleries 3D). Les souffleries numériques ont supplanté les vraies souffleries depuis fort longtemps pour les cas simples car elles sont incomparablement plus faciles et moins coûteuses à mettre en œuvre.

· Les souffleries 3D fonctionnent par éléments finis et résolvent dans le domaine discret les équations de Navier et Stokes. En conséquence, la modélisation prend beaucoup de temps, et hormis sur les grilles de calcul conséquentes, les calculs sont très longs (ils se comptent en heures, voire en jours). Ce type d’outil logiciel ─largement utilisé dans le monde professionnel─ est donc pour le moment hors d’atteinte de l’aéromodéliste.

· Les souffleries 2D ne testent que des profils en résolvant des équations linéaires. Elles sont donc rapides et peuvent se contenter d’un PC pour fonctionner. Il en existe des payantes et des gratuites. Dans le domaine des faibles Reynolds, nous avons la chance de disposer de deux souffleries gratuites :

o Xfoil [7], écrit par l’équipe de Mark Drela du MIT (USA). Ce logiciel est ancien, mais très précis. C’est le seul capable de prendre en compte la formation de bulles sur l’extrados (voir paragraphe suivant). Son inconvénient vient du fait qu’il est écrit pour des systèmes Unix en mode texte, ce qui le rend assez difficile à utiliser, d’autant plus que sous Windows il n’est pas possible de lui passer des scripts. Il n’est pas décrit dans cet ouvrage malgré ses qualités indéniables, car il est plutôt réservé aux spécialistes.

o JavaFoil [8], écrit par Martin Hepperle (Allemagne). Ce logiciel est moderne et conçu d’emblée avec une interface graphique écrite en Java. Il peut soit être téléchargé, soit utilisé directement dans un navigateur internet sous forme d’applet, ce qui le rend extrêmement convivial. Le modèle numérique est un peu moins sophistiqué que celui de Mark Drela, mais il donne malgré tout de bons résultats dans les cas courants. Son plus et sa capacité à simuler plusieurs profils interagissant, ce qui permet d’étudier les interactions entre les plans (utile pour le réglage des biplans comme le réglage des empennages classiques ou canard). Un chapitre spécifique lui est consacré.

La soufflerie numérique 2D permet de faire principalement deux choses :

· étudier le comportement d’un profil (profile donné sous forme de fichier de coordonnées),

· optimiser un profil :

o optimisation directe en modifiant directement le profil de façon itérative jusqu’à obtenir les caractéristiques recherchées,

o optimisation inverse en agissant sur la courbe de pression du profil et en demandant à la soufflerie d’adapter la forme du profil pour respecter la courbe de pression demandée.

Pour aider ceux que ça intéresse à utiliser une soufflerie numérique, JavaFoil va être présenté, mais dans un chapitre ultérieur afin de ne pas alourdir excessivement le présent chapitre déjà très conséquent. Comme cet outil ne permet pas d’analyser les cas spéciaux comme les très faibles et les très hautes vitesses, ces deux cas particuliers vont être effleurés ci-après d’un point de vue strictement théorique.

Aérodynamique des faibles vitesses

L’effet Coanda est la tendance d’un flux d’air à coller spontanément aux surfaces. Cet effet est d’autant moins marqué que le nombre de Reynolds est faible. Aux nombres de Reynolds habituels en modélisme l’écoulement colle assez bien, mais dans le cas des nombres de Reynolds en dessous de 150 000 (vol indoor, slowflier, lancer main, etc.) l’effet Coanda s’estompe. Dans ce dernier cas, en dessous du nombre de Reynolds dit critique, une bulle d’air aplatie se forme (voir figure 30) derrière le point d’épaisseur maximal du profil. Tout le long de cette bulle il n’y a plus de variation de pression et donc de portance. A l’arrière de la bulle un écoulement turbulent de forte épaisseur prend naissance. Le fonctionnement d’une aile dans ce domaine est affecté de plusieurs façons :

· la traînée augmente significativement,

· la portance diminue fortement (typiquement de 30 %),

· le centre de portance se déplace (ce qui perturbe le contrôle),

· une faible augmentation supplémentaire de l’incidence de l’aile provoque un décollement total du flux d’air et donc un décrochage.

Figure 30 : écoulement subcritique avec formation d’une bulle

L’entrée dans le domaine des faibles vitesses ─dit subcritique─ et sa sortie se font avec une forte hystérésis. Ceci signifie qu’un profil ordinaire va entrer dans le domaine subcritique lorsqu’on descend en dessous de 75 000 Reynolds, mais n’en sortira typiquement qu’après une remontée au-delà de 150 000 Reynolds.

Le nombre de Reynolds à partir duquel on entre dans le domaine subcritique peu être significativement diminué (divisé typiquement par deux) en diminuant le rayon de courbure du bord d’attaque et en utilisant un profil mince (figures 31 et 32). Il existe des profils spécifiques pour ces très faibles nombres de Reynolds, surtout utilisés en vol libre.

Figure 31 : profil type PMC19 pour très faibles Reynolds et forte plage de vitesses

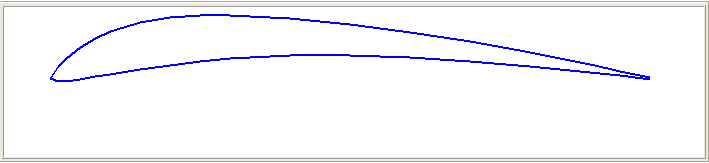
Figure 32 : profil type 20-32C pour très faibles Reynolds et faible plage de vitesses

On peut aussi améliorer fortement un profil classique en redonnant de l’énergie à la couche limite à l’aide d’un « turbulateur ». Un turbulateur est typiquement une bande adhésive de faible largeur et 0,4 mm d’épaisseur placée aux environs de 20 % à 30 % de la corde après le bord d’attaque. Dans ce domaine, les imperfections générant des turbulences ont un effet positif. L’hélice, grande génératrice de turbulence devant l’éternel, soufflant sur l’aile, protège en général du passage dans le domaine subcritique.

Les modèles indoor sont en plein dans le domaine subcritique, mais semblent pourtant y échapper. C’est probablement grâce à l’effet combiné du profil planche à bord d’attaque droit fortement générateur de turbulences et de l’hélice. D’ailleurs, quand on coupe le moteur, la forte tendance des modèles à plonger vers le sol semble démontrer qu’on passe alors dans le domaine subcritique. Malheureusement aucune étude ne semble a priori avoir été faite dans ce domaine.

N. B. : la soufflerie numérique Xfoil est une des rares capable de prendre en compte la formation de bulles et donc d’étudier les profils aux très faibles nombres de Reynolds dans certains cas.

Aérodynamique des hautes vitesses

La vitesse de nos aéromodèles varie typiquement de 10 km/h à 150 km/h (voir chapitre « domaine de vol de nos aéromodèles »), mais peut atteindre 300 km/h en course aux pylônes et même 500 km/h pour certains modèles à réaction. Ce ne sont pas des "hautes vitesses" au sens aérodynamique. On parle de hautes vitesses en aérodynamique lorsque la compressibilité de l’air entre en jeu, donc lorsqu’on s’approche de la vitesse du son. Dans les conditions de température et pression normales les problèmes de compressibilité liés à l’approche de la vitesse du son apparaissent vers 700 km/h. Les hautes vitesses ne concernent donc pas l’aéromodélisme « ordinaire ». Ceci étant écrit, il ne faut pas perdre que de vue que la vitesse à l’extrémité des pales des hélices est souvent de 700 km/h (voir le chapitre sur la propulsion), justement pour ne pas entrer dans le domaine des hautes vitesses. Les racers ne peuvent guère se contenter de vitesses "aussi faibles", leurs hélices fonctionnent donc dans le domaine des hautes vitesses, c'est-à-dire dans le domaine transsonique.

L’air est accéléré sur l’extrados des profils. Il en résulte qu’au-delà de Mach 0,7 (0,7 fois la vitesse du son, soit 850 km/h en conditions normales au sol) l’air dépasse en général le mur du son à l’extrados avec un ensemble de conséquences négatives (traînée d’onde, bruit important, etc.). Pour minimiser les effets négatifs dans ce domaine de vitesses on a donc tout intérêt à utiliser des profils spéciaux dits supercritiques (voir figure 33). Les profils supercritiques sont des profils relativement minces avec un extrados aplati. Ceci a pour effet principal de diminuer la vitesse de l’air à l’endroit de l’onde de choc supersonique. L’onde de choc est reculée vers l’arrière du profil et son amplitude est fortement diminuée ; mais surtout, la vitesse critique (vitesse à laquelle l’onde de choc apparait) est augmentée d’environ 15 %.

Figure 33 : profil supercritique de type Whitcomb

Les ailes

Différence entre profil et aile

Les ailes de nos modèles n’ont pas une envergure infinie, ce qui rend leurs caractéristiques différentes des profils dont elles découlent. La différence entre profil et aile dépend principalement de l’allongement λ défini par l’équation 6.

(6)

Dans cette équation e représente l’envergure et Sa la surface portante de l’aile.

La limitation de l’allongement rend le comportement des ailes différent de celui du profil d’origine en agissant sur plusieurs points explicités ci-après : la pente de portance, le tourbillon marginal (vortex du saumon), la répartition de la portance le long de l’aile.

Pente de portance

La pente de portance d’un profil appelée ao est toujours environ égale à 0,11 (valeur théorique p²/90). La pente de portance a réelle d’une surface portante (ensemble des deux ailes) d’un modèle peut s’estimer à 5 % près par l’équation empirique 7 dans laquelle ae est la pente de portance effective obtenue en multipliant ao par le périmètre des ailes divisé par de double de l’envergure.

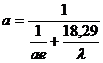(7)

Exemple : soit un modèle d’envergure 1,2 m avec des ailes trapézoïdales de corde 34 cm à l’emplanture et 25 cm au saumon.

· la surface Sa est 12*(3,4 + 2,5)/2 = 35,4 dm²

· L’allongement l est 12*12/35,4 = 4,07

· ae est environ 0,11*(12*2 + 2,5*2)/(12*2) = 0,13

· a est donc finalement égal à 1/(1/1.3 + 18,29/4,07) = 0,083

Pour un planeur à grand allongement a reste très proche de ao = 0,11, tandis que pour une aile delta équilatérale a est égal à 0,046 ; moins de la moitié. Pour une même portance, l’incidence de l’aile delta devra donc être plus du double de celle d’une aile à fort allongement. C’est pour cette raison qu’une incidence de 30° est parfaitement possible avec une aile delta, tandis qu’une aile à fort allongement aura décroché avant l’incidence de 15°.

Tourbillon marginal

L’extrémité des ailes génère un tourbillon marginal source d’une traînée induite (par la portance) dont la valeur réduite Cxi est donnée par l’équation 8 :

(8)

Le coefficient e est le facteur correctif d’Oswald fonction de la forme des ailes. La valeur théorique la plus forte 1 est obtenue pour des ailes elliptiques à incidence constante (pas de vrillage de l’aile entre l’emplanture et le saumon), celles des fameux Spitfire (photo 8). Les avions de transport obtiennent le même résultat en vrillant les ailes (incidence plus forte à l’emplanture qu’aux saumons), mais dans ce cas e n’est égal à 1 que pour une vitesse aérodynamique unique (de l’ordre de 450 km/h). On ne peut dépasser la valeur limite de 1 que par l’ajout de surfaces aérodynamiques spéciales : les winglets (voir plus loin).

Photo 8 : Spitfire de reconnaissance lors du débarquement de juin 1944 (photo Wikipédia)

Noter la forme elliptique des ailes

Comme Cxi est proportionnel au carré de la portance réduite, cette traînée se manifeste surtout à faible vitesse où elle dégrade considérablement la finesse du modèle ; par contre, elle disparaît presque totalement à haute vitesse. On pourra noter également que cette traînée est inversement proportionnelle à l’allongement des ailes, c’est bien sûr ce qui conduit aux très forts allongements des ailes de planeurs qui doivent impérativement minimiser les traînées. D’ailleurs, le point de finesse maximal d’un planeur étant obtenu lorsque la somme des traînées ordinaires (profil, fuselage, empennage, train…) est égale à la traînée induite, aucun aéronef ne peut avoir une finesse dépassant la moitié de celle du profil utilisé. En conséquence, un planeur avec un profil Clark Y de finesse 70 ne pourra jamais dépasser une finesse de 35 du fait de la traînée induite (les planeurs de compétition grandeur actuels atteignent une finesse de 70 et partent donc d’un profil d’une finesse d’environ 150). Pour les modèles autres que les planeurs et moto-planeurs on ne cherche pas à diminuer Cxi en augmentant l’allongement car cela diminue la manœuvrabilité, augmente le poids, augmente le lacet inverse et complique le transport ; on se contente d’effiler plus ou moins des ailes trapézoïdales.

Note à l’intention de ceux qui utilisent les avions de transport : le tourbillon marginal au décollage et à l’atterrissage génère de la traînée parce que c’est un gigantesque brassage de l’air en aval des avions. Ce brassage de même nature que le sillage d’un bateau rend le vol strictement impossible immédiatement en aval. C’est lui qui impose le délai entre l’atterrissage et le décollage de deux avions successifs, ce qui limite la capacité des aéroports.

Répartition de la portance

Avec des ailes de forme non elliptique, à moins de jouer sur le vrillage de l’aile, le Cz n’est pas constant le long des ailes.

Le calcul de la variation Cz le long d’une aile se fait par ordinateur. Nous utiliserons à cette fin le logiciel libre Nurflügel de Michael Möller (aussi auteur du célèbre simulateur de vol libre FMS) initialement destiné aux ailes volantes, capable de faire de nombreux autres calculs. Ce logiciel est décrit en détail dans un chapitre suivant. Pour des ailes rectangulaires d’allongement 6 on obtient l’évolution de Cz présenté sur la figure 34.

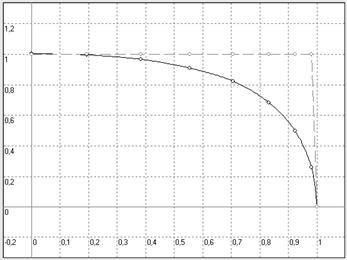
effilement

Figure 34 : variation de la portance réduite Cz le long d’une aile de forme rectangulaire selon le logiciel Nurflügel

La figure 34, représente l’évolution de Cz en fonction de la position le long de l’aile droite d’un modèle. On remarque que pour un Cz max = 1 à l’emplanture Cz diminue au fur et à mesure que l’on s’approche du saumon car l’air a tendance à s’échapper latéralement. Le Cz moyen n’est finalement que de 0,85 dans ce cas. Ceci conduit à définir le coefficient kd de portance, égal au rapport entre le Cz moyen maximal d’une aile divisé par le Cz max du profil utilisé, égal à 0,85 pour notre exemple. Si le Cz max du profil est de 1,2, le Cz max des ailes sera Cz max*kd = 1,2x0,85 = 1,02. Tout se passe donc comme si 15 % de la surface ne générait plus de portance (tout en continuant à générer de la traînée et du poids).

Le coefficient correctif de traînée induite e peut être estimé en première approximation égal à kd, soit ici à 0,85.

A prendre des ailes rectangulaires au lieu d’elliptiques ont a donc perdu sur deux tableaux : perte de portance maximale et augmentation de la traînée induite, mais on a aussi gagné sur deux tableaux : facilité de construction et décrochage sain d’abord au centre. Ce dernier point prend tout son sens si on rappelle qu’en cas de décrochage initial à l’emplanture des ailes, le modèle a tendance à partir droit vers le bas, alors que dans le cas contraire, une aile décroche toujours avant l’autre et c’est le départ en vrille souhaité ou non.

Les ailes rectangulaires n’étant pas optimales et les ailes ellipsoïdales difficiles à construire, la forme la plus courante pour une aile est la forme trapézoïdale, bon compromis entre performance et facilité de construction. Avec un effilement de 20 à 50 % (diminution de la corde au saumon par rapport à l’emplanture), l’efficacité augmente avec l’effilement et le comportement reste acceptable. Avec un effilement de plus de 50 % les départs en vrille incontrôlée sont à craindre.

Le tableau 1 donne les kd valeurs approximatives pour les principaux degrés d’effilement d’ailes trapézoïdales d’allongement 6.

effilement	0 %	20 %	33 %	50 %	65 %
kd	0,86	0,9	0,91	0,92	0,9

Tableau 1 : portance relative en fonction de l’effilement d’une aile

Avec des ailes faites de deux ou trois panneaux pour se rapprocher de la forme elliptique (série des planeurs Discus) on obtient quasiment le même résultat qu’une ellipse, mais ça n’a d’intérêt que pour un planeur qui a besoin d’une finesse maximale.

Avec une aile strictement triangulaire, Cz augmente de façon catastrophique au saumon, ce qui est très néfaste au comportement. C’est pourquoi les ailes delta modernes ont toujours l’extrémité des ailes rognées. Une aile delta d’envergure 1,2 m, de corde 90 cm à l’emplanture et 15 cm au saumon donne kd ≈ 0,73.

Surfaces de contrôle

A moins d’une géométrie spéciale (ailes volantes) il faut des surfaces supplémentaires (petites ailes) pour rendre un aéronef à la fois stable, c'est-à-dire capable de conserver une direction de vol donnée et manœuvrable, c'est-à-dire capable de changer de direction en fonction d’une commande.

La stabilité est obtenue (sauf pour les ailes volantes) en ajoutant une surface verticale à l’arrière appelée empennage vertical et une surface horizontale appelée empennage horizontal. Cet empennage horizontal normalement placé à l’arrière peut aussi être placé à l’avant, auquel cas il s’appelle empennage canard (si quelqu’un peut expliquer le rapport avec les canards il est le bienvenu).

La manœuvrabilité est obtenue en changeant ponctuellement la portance des ailes et empennages. Le galbe, i.e. la courbure relative d’un profil est l’élément influant le plus sur la portance. Donc, changer la courbure revient à régler la portance. Les premiers avions utilisaient donc le gauchissement des surfaces, mais on s’est rapidement aperçu qu’il était possible d’obtenir le même résultat de façon beaucoup plus simple en rendant mobile une partie du bord de fuite des surfaces.

Ailerons

Les ailerons permettent de diminuer ou d’augmenter la portance d’une aile. Ils fonctionnent évidement de façon symétrique. On baisse un aileron lorsqu’on relève l’autre, ce qui augmente la portance d’une des ailes tout en diminuant d’autant celle de l’autre. Il s’en suit le basculement à gauche ou à droite du modèle, ce qui le met en virage.

On distingue deux types de d’ailerons :

· les ailerons classiques qui s’étendent sur la moitié externe de chaque aile avec une corde d’environ le quart de celle de l’aile,

· les ailerons "full span" (pleine envergure) qui s’étendent sur toute l’envergure mais avec une corde deux fois plus faible que celle des ailerons classiques.

En vol normal il n’y a pas grande différence entre les deux ; l’aileron dit full span ayant toutefois l’avantage d’être plus facilement commandé par un servomoteur central unique. Par contre, en vol 3D il y une différence importante. Les ailerons full span sont soufflés par l’hélice et gardent donc une partie de leur efficacité à l’arrêt, ce qui n’est pas le cas des autres qui deviennent totalement inefficaces en vol stationnaire. Par contre, il est impossible d’utiliser des volets full span si on veut mettre des volets d’atterrissage (à moins d’utiliser un mixage électronique).

En vol indoor, seuls les ailerons full span avec une forte corde sont utilisables car l’efficacité des ailerons diminue avec la vitesse.

Empennage vertical

L’empennage vertical aussi appelé dérive par analogie avec la surface correspondante des bateaux à voile a le même rôle que celui des plumes de l’empennage des flèches, à savoir reculer le centre de portance derrière le centre de masse afin que la flèche (ou le modèle) ne tourbillonne pas autour de son centre de masse. Dans un aéromodèle, la dérive compense l’effet déstabilisant de l’avant du fuselage. Cette surface devra donc être d’autant plus grande que le fuselage se prolongera loin devant les ailes. Dans le cas des avions grandeur multi-moteurs la dérive est agrandie car il faut pouvoir compenser le couple de lacet généré par un éventuel moteur en panne. Le dimensionnent de la dérive est approfondi dans le chapitre sur la stabilité.

Empennage horizontal

L’empennage horizontal a la même fonction stabilisatrice que la dérive, mais la détermination est plus critique car il faut compenser le couple de basculement des ailes et ne pas induire un mauvais comportement en décrochage. De plus, la fonction "manœuvrabilité" est beaucoup plus importante que dans le cas de la dérive.

Les avions des pionniers utilisaient des empennages horizontaux justes suffisants pour compenser le couple de basculement des ailes, mais ils entrainaient des pertes de contrôle dans les situations critiques. Sur un aéromodèle classique, l’empennage est largement surdimensionné par rapport à ce besoin critique. Une surface de l’ordre du quart des celle des ailes est typiquement retenue pour avoir un bon amortissement et une bonne efficacité de la commande de profondeur.

L’allongement est choisi toujours inférieur à celui des ailes de façon que le coefficient de pente de portance soit plus faible que celui des ailes. Ainsi, les ailes décrochent en premier, ce qui provoque un basculement vers l’avant et évite la vrille à plat incontrôlable.

Dans la configuration normale, c’est-à-dire empennage horizontal à l’arrière, comme les ailes ont tendance à basculer vers l’avant du fait de leur courbure et de la position du centre de masse, l’empennage horizontal doit pousser vers le bas pour compenser le moment de basculement. Les ailes sont donc obligées de fournir une portance supplémentaire pour compenser cette déportance. C’est ce qui justifie l’empennage horizontal à l’avant (dit canard), car dans ce dernier cas l’empennage est porteur, ce qui soulage les ailes. Malgré cet avantage les empennages canard sont peu utilisés car leur détermination est délicate. En effet, l’empennage canard doit décrocher avant les ailes pour éviter la vrille à plat, mais pas trop tôt pour pouvoir bénéficier de toute la portance des ailes. Cela conduit à des empennages canard très galbés et à fort allongement (pour augmenter la pente de portance) et de surface juste suffisante ; la difficulté étant précisément de trouver la valeur de surface "juste".

Surfaces secondaires

Les volets et aérofreins

La figure 35 montre l’effet de trois réglages de volets sur un profil S3021: bas pour gratter, neutre pour transiter, haut pour pénétrer. On peut aussi incliner les volets à 45° ou plus, ce qui a pour effet d’augmenter considérablement la traînée et donc d’accélérer la descente. C’est un artifice très utile pour simplifier les atterrissages. Presque tous les avions grandeur utilisent ce principe.

Figure 35 : évolution de la polaire d’un profil S3021 selon la position du volet de courbure.

Caractéristiques obtenues avec la soufflerie numérique JavaFoil.

Sur les avions de transport grandeur on pousse même le jeu à l’extrême en ajoutant bec de bord d’attaque et volets à double (voire triple) fente. Les fentes du bec et des volets permettent de canaliser l’air et retarder le décollement du flux. Ca permet d’atteindre un C zmax supérieur à 4, et ainsi atterrir comme une fleur à "à peine 250 km/h" si les réservoirs sont au niveau bas malgré la charge alaire. La reproduction maquette de ces volets au mécanisme compliqué est un challenge intéressant !

On utilise aussi des aérofreins de formes diverses sur le fuselage et les ailes pour augmenter le taux de chute. Si ça crée des turbulences, ça marche ! Le problème est parfois le couple de basculement induit. Sur les planeurs, baisser les volets centraux et lever les volets externes s’appelle position « crocodile » (butterfly en anglais) et produit le même effet.

Winglets et autres artifices d’extrémité d’aile

Les tourbillons d’extrémité d’aile génèrent une traînée qui dépasse toutes les autres à faible vitesse. Ils ont donc toujours chagriné les aérodynamiciens, professionnels comme amateurs qui voudraient les limiter, d’où l’invention nombreuses verrues (photo 9) plus ou moins efficaces à ajouter aux ailes. Il faudrait un article complet rien que pour en exposer les tenants et aboutissants. On se contentera de mentionner ici le fait qu’on peut espérer gagner environ 10 % de traînée induite si on se débrouille bien.

Photo 9 : winglet d’Airbus (photo Wikipédia)

Artifices aérodynamiques divers

Un écoulement peut se décoller sans prévenir, devenir turbulent et casser l’aérodynamique d’un modèle même s’il est bien profilé (voir paragraphe sur la traînée). Nous allons donner ici quelques exemples.

L’intersection aile/fuselage est particulièrement problématique. La mise en place d’arrondis appelés Karman (du nom de l’aérodynamicien qui les a inventés) est parfois une nécessité (voir photo 4).

Il est notoire que sur un fuselage, même parfaitement profilé, l’écoulement peut parfois devenir instable, osciller de droite à gauche derrière le cockpit suite à un phénomène de résonance. Un petit dispositif capable d’amortir l’oscillation comme une crête sur le dos du fuselage devant la dérive peut stopper cette oscillation. La fameuse mini-aile des Paysant Le Roux agit probablement de la sorte.

Il y a une multitude de ces dispositifs sur les avions grandeur ajoutés suite à des essais en soufflerie. On les retrouve sur les maquettes où ils ne remplissent en général pas du tout leur office car le nombre de Reynolds est très différent.

Détermination des ailes

Déterminer des ailes revient à choisir dans l’ordre les divers paramètres suivants en fonction des critiques développés dans les paragraphes correspondants :

1. le profil en fonction de l’utilisation (planeur, entraînement, racer, acrobatie…),

2. la forme en fonction de l’utilisation (tendance à la vrille) et de l’esthétique,

3. l’allongement en fonction de la finesse et la manœuvrabilité désirée (3 pour le vol 3D, 4 à 6 pour un aéromodèle ordinaire, au-delà pour un planeur selon l’envergure retenue),

4. la surface en fonction du Cz max défini par les paramètres 1 à 3 et la plage de vitesse retenue en fonction du type d’aérormodèle.

La réalisation de ce travail à la main n’est plus très pertinente aujourd’hui. On utilisera bien sûr Aérocalc (ou la feuille de calcul équivalente) qui permettra de faire facilement la synthèse en s’aidant de Javafoil (ou équivalent) et Nurflügel (ou équivalent).

Le fuselage

Fonctions

Le fuselage sert à relier ensembles les ailes, empennage, moteur et train d’atterrissage, tout en contenant le système de réception radio et les sources d’énergie et de commande du moteur. Comme il a typiquement une influence négative sur l’aérodynamique on cherche à minimiser sa taille dans les modèles de compétition (planeur, racer) voire à le faire disparaitre en utilisant la formule « aile volante ».

Toutefois dans certains cas, il a un effet bénéfique sur le comportement aérodynamique. En particulier, dans le cas de la voltige aérienne, le fuselage est essentiel pour le vol tranche car il remplace alors les ailes. C’est ce qui explique les gros fuselages très hauts et plats des modèles de type F3A et dérivés. Toujours dans le même domaine de l’aéromodélisme, la longueur contribue à améliorer l’amortissement et donc la propreté des figures, ce explique la grande longueur sur les modèles d’acrobatie.

Traînée

La traînée des ailes est principalement une traînée de friction (sauf à fort Cz près du décrochage) donnée par la polaire des ailes Cxp, additionnée de la traînée induite Cxi définie par l’équation 8. La traînée du fuselage Cxf est aussi une traînée de friction si aucun décollement ne se manifeste. Malheureusement, dans ce cas précis il n’y a pas de polaire à disposition. Une méthode empirique qui donne des résultats satisfaisants consiste à utiliser l’équation 9 :

(9)

Dans cette équation Cxp min est le Cx minimal du profil d’aile du modèle, tandis que Cxp est le Cx du profil d’aile à l’incidence considérée. Prendre le Cx de l’aile comme référence peut paraître étrange, voir incongru, mais il ne faut pas perdre de vue qu’ailes et fuselage sont en principe en harmonie. Qui mettrait un fuselage caisse mal dégrossi sur un planeur tout composite ou l’inverse ? Cxp est là pour tenir compte du fait qu’à forte incidence le Cx du fuselage se dégrade aussi, mais nettement moins que celui des ailes. Sf, Sa, Sd et Ss sont respectivement : surface mouillée du fuselage, surface portante des ailes, dérive et stabilisateur. La formule intègre donc les traînées de l’empennage.

Dans cette équation 9, Cxf est normalisé à la surface des ailes Sa. Ainsi, Cxf pourra être ajouté directement au Cx des ailes et être utilisé dans l’équation de traînée sans autre forme de procès pour fournir la traînée cumulée, avec comme référence de surface unique celle des ailes.

On pourra arguer que le nombre de Reynolds du fuselage n’est pas le même que celui des ailes. Mais si celui du fuselage est supérieur, il est compensé par celui, inférieur, de l’empennage. De toutes façons le coefficient k, dernier élément de la formule, permet de tenir compte de ce fait. Ce coefficient est là pour tenir compte de tous éléments perturbateurs du fuselage qui augmentent sa traînée. Pour un fuselage de maquette de planeur en composite sans défaut il ne faut pas hésiter à prendre k = 1. Pour un avion ordinaire avec des vis de fixation d’aile, une antenne, et des commandes de gouverne non carénées k = 1,5 convient bien. C’est la valeur obtenue sur la version grandeur de P38. Sur un fuselage peu soigné (moteur non caréné) k peut atteindre 2.

L’équation empirique 9 ne peut pas prétendre à une grande précision, mais elle est en général suffisante et il est de toutes façons difficile de trouver plus précis à moins d’utiliser une soufflerie.

L’équation 9 nécessite la surface mouillée du fuselage qui pourra être obtenue à l’aide d’Aérocalc, d’une feuille de calcul ou le calcul manuel. Si on n’utilise pas Aérocalc, on pourra pour simplifier le calcul utiliser aussi une formule empirique (équation 10).

(10)

Dans cette équation, h, l et L sont respectivement la hauteur du maître couple, la largeur du maître couple et la longueur du fuselage. Le coefficient ks est le coefficient de section qui permet d’obtenir le périmètre d’une section du fuselage en fonction de sa hauteur et de sa largeur. Il est égal à 1 pour un fuselage caisse, à 0,78 pour un fuselage parfaitement elliptique et entre ces deux valeurs dans les autres cas.

Le coefficient kp correspond au coefficient de profilage. Il est égal à 1 pour un profil de fuselage rectangulaire, ce qui, contrairement aux apparences existe ; au moins un modéliste ayant réalisé un fuselage en cannettes de bière accolées et on pourrait parfaitement imaginer un fuselage constitué exclusivement de barreaux de batteries. Plus sérieusement, la figure36 indique les coefficients kp de quelques profils de fuselages classiques dont on pourra s’inspirer pour estimer le coefficient kp de son propre fuselage.

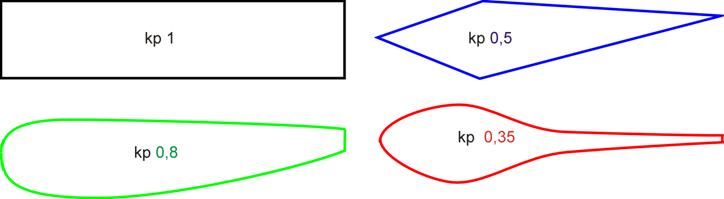
profilage

Figure 36 : coefficient de profilage d’un fuselage selon sa forme

L’équation 9 ne tient pas compte des éléments non carénés du fuselage comme le train d’atterrissage. Il faut donc calculer leur produit Cx.S, le normaliser à la surface Sa des ailes et ajouter la valeur obtenue à Cxf.

Si on utilise Aérocalc, on n’a pas besoin des ces équations simplificatrices, car le logiciel fait un calcul précis des surfaces.

Moment d’inertie

La masse m d’un corps représente sa résistance au déplacement imposé par une force extérieure F selon la célèbre loi de Newton F = m.g, g représentant l’accélération du corps engendré par la force F. Il découle de cette formule qu’un aéromodèle sera d’autant moins « chahuté » qu’il est lourd. Soit, mais les turbulences provoquent aussi un mouvement de rotation (donc de basculement) autour du centre de masse beaucoup plus gênant que le mouvement de translation en raison de son influence sur la trajectoire future de l’aéromodèle. Pour calculer l’effet en rotation il existe une loi semblable à la loi de Newton: M = J.w’ dans laquelle M est le moment de rotation (force de rotation imposée), J le moment d’inertie et w' l’accélération angulaire résultante. Or, s’il est impossible d’influer sur la masse d’un aéromodèle dans la mesure où il s’agit d’un choix initial, il est possible sans changer la masse d’influer sur son moment d’inertie J et donc sur sa propension à changer de direction.

Cette observation signifie qu’il est possible de faire en sorte qu’un modèle se comporte comme un modèle plus gros (donc plus stable) en augmentant son moment d’inertie ou plus petit (plus dynamique) en le diminuant. Cette possibilité est peu exploitée en modélisme, mais mérite pourtant qu’on s’y intéresse.

Le moment d’inertie j d’un élément ponctuel de masse m distant d’une longueur l du centre de rotation est j = m.l², ce qui signifie que le moment d’inertie est proportionnel au carré de la distance au centre de rotation. Le moment d’inertie d’un aéromodèle complet est la somme des moments d’inertie de chaque élément et est donc donné par l’équation 11 :

(11)

L’interprétation de l’équation 11 doit se faire de la façon suivante : si tous les éléments sont concentrés près du centre de masse, l’inertie est très faible. Elle est augmentée à chaque fois qu’on éloigne un élément du centre de masse.

On peut être plus précis et considérer quatre types d’éléments :

· les éléments libres (servos, batteries, récepteur…) que l’on peut déplacer à volonté,

· le fuselage proprement dit sur lequel on ne peut guère influer,

· la queue avec son empennage qui déséquilibre le modèle vers l’arrière,

· le moteur avec ses accessoires qui compense de poids de la queue.

Dans cet ensemble la queue est un élément critique car on compense son poids en écartant le moteur du centre de masse. Dans le cas d’un planeur le moteur est remplacé par un contrepoids ou les batteries de réception, mais ça revient au même. Si on alourdit la queue il faut avancer le moteur pour compenser, les autres éléments pouvant être proches du centre de masse. Par contre, si on allège la queue on peut mieux concentrer les divers éléments au centre de masse et diminuer le moment d’inertie.

Les avions de la première guerre mondiale avaient une queue entoilée très légère (photo 1) ce qui permettait de placer le moteur très près du centre de masse. Ainsi l’avion avait un très faible moment d’inertie, ce qui le rendait plus mobile et facilitait les manœuvres évasives.

Aérocalc prend en compte le moment d’inertie pour déterminer la stabilité dynamique (voir chapitre correspondant).

Détermination d’un fuselage

La forme d’un fuselage est avant tout une question d’esthétique. Mais dans le cas d’un racer ou un planeur, le fuselage sera le plus petit possible et de section circulaire de façon à limiter la surface mouillée et donc la trainée. Pour un avion de voltige on choisira un fuselage haut et plat pour le vol tranche. Pour un avion d’entrainement la forme caisse simplifiera la construction. Dans le cas d’une maquette, la forme est toute trouvée…

La longueur d’un fuselage vers l’arrière est déterminée pas le degré d’amortissement en tangage désiré. Pour un modèle standard une valeur courante est la longueur entrainant un bras de levier (distance entre le foyer des ailes et de l’empennage) de trois fois la corde moyenne des ailes ; un fuselage plus court rendant le modèle moins agréable à contrôler. En F3A on prend la valeur la plus forte autorisée par le règlement pour maximiser l’amortissement.

La longueur d’un fuselage vers l’avant est définie par la position du moteur dont la masse doit équilibrer l’aéromodèle. Le calcul se fait assez facilement par approximations successives en utilisant Aérocalc.

Références

John D. Anderson Jr, "A History of aerodynamics", Cambridge University Press, 1997
Site d’Alain Vassel, Epilogue sur Clément Ader
P38 Lightning, Wikipédia
Alberto Santos-Dumont, célèbre pionnier Brésilien inventeur de la montre bracelet et constructeur de la "Demoiselle"
Effet Coanda, Wikipédia
Charles Fauvel, ingénieur aéronautique français
Xfoil, soufflerie numérique de Mark Drela (MIT)
JavaFoil, soufflerie numérique de Martin Hepperle